Welcome to Ganitsarani

1.

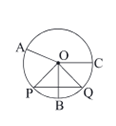
পাশের O কেন্দ্রীয় বৃত্তের ছবি দেখি এবং কোন কোন ব্যাসার্ধ PAQ বৃত্তাংশে অবস্থিত লিখি ।

2. নীচের ______ এ বুঝে লিখি:

(i) একটি বৃত্তে \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) বিন্দু আছে।
(ii) বৃত্তের বৃহত্তম জ্যা \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) ।
(iii) জ্যা বৃত্তাকার ক্ষেত্রকে দুটি \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) বিভক্ত করে ।
(iv) বৃত্তের সকল ব্যাস \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) বিন্দুগামী ।
(v) দুটি বৃত্তাংশ সমান হলে তাদের বৃত্তচাপ দুটির দৈর্ঘ্য \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) হবে ।
(vi) একটি বৃত্তাকার ক্ষেত্রের বৃত্তকলা হলো বৃত্তচাপ এবং দুটি \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\) এর দ্বারা সীমাবদ্ধ অঞ্চল ।
(vii) বৃত্তের বাইরের কোনো বিন্দু ও কেন্দ্রের সংযোজক রেখাংশের দৈর্ঘ্য ব্যাসার্ধের দৈর্ঘ্য অপেক্ষা \(\bbox[white,12px,border:1px solid black] {\,\,\,\,\,\,\,\,\,\,\,}\)।
3. স্কেল ও পেনসিল কম্পাসের সাহায্যে একটি বৃত্ত এঁকে কেন্দ্র, জ্যা, ব্যাস, ব্যাসার্ধ, উপচাপ, অধিচাপ নির্দেশ করি ।

4. সত্য না মিথ্যা লিখি:

(i) স্কেল ও পেনসিল কম্পাসের সাহায্যে একটি বৃত্ত এঁকে কেন্দ্র, জ্যা, ব্যাস, ব্যাসার্ধ, উপচাপ, অধিচাপ নির্দেশ করি ।
(ii) বৃত্ত একটি সামতলিক চিত্র ।
(iii) বৃত্তাংশ (Segment)একটি সামতলিক ক্ষেত্র।
(iv) বৃত্তকলা(Sector)একটি সামতলিক ক্ষেত্র।
(v) জ্যা একটি সরলরেখাংশ ।
(vi) চাপ একটি সরলরেখাংশ ।
(vii) একটি বৃত্তে সসীম সংখ্যক একই দৈর্ঘের জ্যা আছে ।
(viii) একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে একটিই বৃত্ত আঁকা সম্ভব ।

1. O কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং AB একটি একটি জ্যা এর দৈর্ঘ্য 8 সেমি । O বিন্দু থেকে AB জ্যা এর দূরত্ব হিসাব করে লিখি ।
2. O কেন্দ্রীয় একটি বৃত্তের ব্যাসের দৈর্ঘ্য 26 সেমি । O বিন্দু থেকে PQ জ্যা এর দুরত্ব 5 সেমি। PQ জ্যা এর দৈর্ঘ্য হিসাব করে লিখি ।
3. O কেন্দ্রীয় একটি বৃত্তের PQ জ্যা এর দৈর্ঘ্য 4 সেমি এবং O বিন্দু থেকে PQ এর দূরত্ব 2.1 সেমি । বৃত্তের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি ।
4. O কেন্দ্রীয় বৃত্তে 6 সেমি ও 8 সেমি দৈর্ঘ্যের দুটি জ্যা । যদি ছোটো দৈর্ঘ্যের জ্যাটির বৃত্তের কেন্দ্র থেকে দূরত্ব 4 সেমি হয়, তাহলে অপর জ্যাটির কেন্দ্র থেকে দূরত্ব কত তা হিসাব করে লিখি ।
5. যদি কোনো বৃত্তের একটি জ্যা এর দৈর্ঘ্য 48 সেমি এবং কেন্দ্র থেকে ওই জ্যা এর দূরত্ব 7 সেমি হয়, তবে ওই বৃত্তের কেন্দ্র থেকে যে জ্যা-এর দূরত্ব 20 সেমি সেই জ্যা এর দৈর্ঘ্য কত হবে তা হিসাব করে লিখি ।
6. পাশের O কেন্দ্রীয় বৃত্তের ছবিতে OP\(\bot\)AB; AB=6 সেমি এবং PC=2 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।
7. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমান করি যে AC=DB
8. প্রমান করি, কোনো বৃত্তের দুটি পরস্পরছেদি জ্যা পরস্পরকে সমদ্বিখন্ডিত করতে পারে না, যদি না উভয়েই বৃত্তের ব্যাস হয় ।
9. X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । XY-এর মধ্যবিন্দু S-এর সঙ্গে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে SA-এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করল । প্রমান করি যে PA=AQ.
10. O কেন্দ্রীয় বৃত্তের 10 সেমি ও 24 সেমি দৈর্ঘ্যের দুটি সমান্তরাল জ্যা AB এবং CD কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। যদি AB ও CD-জ্যা দুটির মধ্যে দূরত্ব 17 সেমি হয়, তবে হিসাব করে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য লিখি ।
11. দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্তদুটি A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করি যে, CD=2PQ.
12. একটি বৃত্তের AB ও AC জ্যা দুটি সমান। প্রমাণ করি যে, \(\angle\)BAC -এর সমদ্বিখন্ডক কেন্দ্রগামী।
13. একটি বৃত্তের দুটি পরস্পরছেদী জ্যা-এর অন্তর্ভূক্ত কোণের সমদ্বিখন্ডক যদি কেন্দ্রগামী হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি সমান।
14. প্রমাণ করি, একটি বৃত্তে দুটি জ্যা-এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবর্তী সেটির দৈর্ঘ্য অপর জ্যা-টির দৈর্ঘ্য অপেক্ষা বৃহত্তর।
15. একটি বৃত্তের ভিতর যে-কোনো বিন্দু দিয়ে ক্ষুদ্রতম জ্যা কোনটি হবে তা প্রমাণ করে লিখি ।

16. অতিসংক্ষিপ্র উত্তরধর্মী প্রশ্ন (V.S.A)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)

(i) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান । \(\angle\)AOB=60° হলে \(\angle\)COD এর মান

(a) 40° (b) 30° (c) 60° (d) 90°

(ii) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং বৃত্তের একটি জ্যা-এর দৈর্ঘ্য 10 সেমি। বৃত্তের কেন্দ্র থেকে জ্যা-এর দূরত্ব

(a) 12.5 সেমি (b) 12 সেমি (c) √69 সেমি (d) 24 সেমি

(iii) O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা । O বিন্দু থেকে AB জ্যা-এর দূরত্ব 4 সেমি হলে, CD জ্যা-এর দুরত্ব

(a) 2 সেমি (b) 4 সেমি (c) 6 সেমি (d) 8 সেমি

(iv) AB ও CD দুটি সমান্তরাল জ্যা-এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি । বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি হলে, জ্যা দুটির মধ্যে দুরত্ব

(a) 12 সেমি (b) 16 সেমি (c) 20 সেমি (d) 5 সেমি

(v) দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O; একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। AC=5 সেমি হলে BD-এর দৈর্ঘ্য

(a) 2.5 সেমি (b) 5 সেমি (c) 10 সেমি (d) কোনোটিই নয়

(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি ।

(i) তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায় ।
(ii) ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত।
(iii) O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, \(\angle\)OAB=\(\angle\)OAC

(C) শূন্যস্থান পূরণ করি।

(i) O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1:1 হলে, \(\angle\)POQ : \(\angle\)ROS = _____ |
(ii) বৃত্তের কোনো জ্যা-এর লম্বসমদ্বিখন্ডক ওই বৃত্তের _______ ।

11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)

(i) 10 সেমি দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারণ জ্যা- এর দৈর্ঘ্য 12 সেমি। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব নির্ণয় করি ।
(ii) 5 সেমি দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্তে AB এবং AC দুটি সমান দৈর্ঘ্যের জ্যা। বৃত্তের কেন্দ্র ABC ত্রিভুজের বাইরে অবস্থিত। AB=AC=6 সেমি হলে, BC জ্যা-এর দৈর্ঘ্য নির্ণয় করি।
(iii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। \(\angle\)AOB=60° এবং CD=6 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করি।
(iv) O কেন্দ্রীয় বৃত্তের ভিতর P যে-কোনো একটি বিন্দু। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি, এবং OP=3 সেমি হলে, P বিন্দুগামী যে জ্যাটির দৈর্ঘ্য ন্যূনতম তা নির্ণয় করি ।
(v) P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত A ও B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ-এর সমান্তরাল সরলরেখা বৃত্তদুটিকে যথাক্রমে C ও D বিন্দুতে ছেদ করে। PQ=5 সেমি হলে, CD-এর দৈর্ঘ্য কত তা নির্ণয় করি ।

A. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করো :

1. O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান, \(\angle\)AOB=60° হলে, \(\angle\)COD এর মান হবে — (a) 30° (b) 60° (c) 120° (d) 180°মাধ্যমিক-2020

B. সত্য বা মিথ্যা লেখো :

1. তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত আঁকা যায় ।মাধ্যমিক-2019

C. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :

1. 5 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্তের দুটি সমান্তরাল জ্যা-এর দৈর্ঘ্য 6 সেমি ও 8 সেমি। জ্যা দুটির দূরত্ব কত ?মাধ্যমিক-2009
2. O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী । ∠AOB=60° এবং CD = 6 সেমি হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য কত ?মাধ্যমিক-2018
3. O-কেন্দ্রীয় বৃত্তের ব্যাসার্ধ 10 সেমি। O থেকে বুত্তের একটি জ্যা AB-এর উপর অঙ্কিত লম্বের দৈর্ঘ্য 6 সেমি হলে AB জ্যা-এর দৈর্ঘ্য কত?মাধ্যমিক-2004

D. রচনাধর্মী প্রশ্ন :

1. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে । প্রমাণ করো, AC = BD ।মাধ্যমিক-2018, 2011
2. প্রমাণ করাে যে, ব্যাস নয় এরূপ কেনাে জ্যা-কে বৃত্তের কেন্দ্রগামী কোনাে সরলরেখাংশ সমদ্বিখণ্ডিত করলে, ঐ সরলরেখাংশ জ্যা-এর উপর লম্ব হবে। মাধ্যমিক-2016, 2012
3. প্রমান করো যে, কোনো বৃত্তের দুটি সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী ।মাধ্যমিক-2006
4. প্রমান করো যে, ব্যাস নয় এরূপ কোনো জ্যা-এর উপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করা হলে, ঐ লম্ব জ্যা-কে সমদ্বিখন্ডিত করবে ।মাধ্যমিক-2006, 2022