Welcome to Ganitsarani
সদৃশতা
কষে দেখি 18.1 [উত্তর দেখতে Question এর ওপর Click করুন ]
Top
1. ______-এ সঠিক উত্তর লিখি:
(i) সকল বর্গক্ষেত্র ______ [সর্বসম / সদৃশ]
(ii) সকল বৃত্ত ______ [সর্বসম / সদৃশ]
(iii) সকল ______ [সমবাহু/ সমদ্বিবাহু] ত্রিভুজ সর্বদা সদৃশ।
(iv) দুটি চতুর্ভুজ সদৃশ হবে যদি তাদের অনুরূপ কোণগুলি ______ [সমান / সমানুপাতী] হয় এবং অনুরূপ বাহুগুলি ______ [অসমান / সমানুপাতী] হয়।
2.নীচের বাক্যগুলি সত্য না মিথ্যা লিখি :
(i) যে-কোনো দুটি সর্বসম চিত্র সদৃশ।
(ii) যে-কোনো দুটি সদৃশ চিত্র সর্বদা সর্বসম।
(iii) যে-কোনো দুটি সদৃশ বহুভুজাকার চিত্রের অনুরূপ কোণগুলি সমান।
(iv) যে-কোনো দুটি সদৃশ বহুভুজাকার চিত্রের অনুরূপ বাহুগুলি সমানুপাতিক।
(v) বর্গক্ষেত্র ও রম্বস সর্বদা সদৃশ।
3. একজোড়া সদৃশ চিত্রের উদাহরণ লিখি।
4. একজোড়া চিত্র অঙ্কন করি যারা সদৃশ নয়।
কষে দেখি 18.2 [উত্তর দেখতে Question এর ওপর Click করুন ]
Top
1. ∆ABC-এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
(i) PB = AQ, AP= 9 একক, QC = 4 একক হলে, PB-এর দৈর্ঘ্য হিসাব করে লিখি।
(ii) PB-এর দৈর্ঘ্য AP-এর দৈর্ঘ্যের দ্বিগুণ এবং QC-এর দৈর্ঘ্য AQ-এর দৈর্ঘ্যের চেয়ে 3 একক বেশি হলে, AC-এর দৈর্ঘ্য কত হবে, হিসাব করে লিখি।
(iii) যদি AP = QC, AB-এর দৈর্ঘ্য 12 একক এবং AQ-এর দৈর্ঘ্য 2 একক হয়, তবে CQ-এর দৈর্ঘ্য কত হবে, হিসাব করে লিখি।
2. ∆PQR-এর PQ ও PR বাহুর উপর যথাক্রমে X, Y দুটি বিন্দু নিলাম।
(i) PX = 2 একক, XQ = 3.5 একক, YR = 7 একক এবং PY = 4.25 একক হলে, XY ও QR পরস্পর সমান্তরাল হবে কিনা যুক্তি দিয়ে লিখি।
(ii) PQ = 8 একক, YR = 12 একক, PY = 4 একক এবং PY-এর দৈর্ঘ্য XQ-এর দৈর্ঘ্যের চেয়ে 2 একক কম হলে, XY ও QR সমান্তরাল হবে কিনা যুক্তি দিয়ে লিখি।
3. প্রমাণ করি যে, কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে। [থ্যালেসের উপপাদ্যের সাহায্যে প্রমাণ করি]
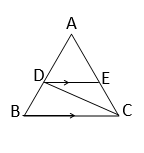
4. ∆ABC-এর AD মধ্যমার উপর P একটি বিন্দু। বর্ধিত BP ও CP যথাক্রমে AC ও AB-কে Q ও R বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, RQ || BC.
5. ∆ABC-এর BE ও CF মধ্যমাদুটি পরস্পরকে G বিন্দুতে ছেদ করেছে এবং FE সরলরেখাংশ AG সরলরেখাংশকে O বিন্দুতে ছেদ করলে, প্রমাণ করি যে AO = 3OG.
6. প্রমাণ করি যে, ট্রাপিজিয়ামের তির্যক বাহুগুলির মধ্যবিন্দু দুটির সংযোজক সরলরেখাংশ সমান্তরাল বাহুগুলির সমান্তরাল।
7. ∆ABC-এর BC বাহুর উপর D যে-কোনো একটি বিন্দু। P, Q যথাক্রমে ∆ABD ও ∆ADC-এর ভরকেন্দ্র। প্রমাণ করি যে, PQ || BC.
8. একই ভূমি QR-এর উপর এবং একই পার্শ্বে দুটি ত্রিভুজ ∆PQR ও ∆SQR অঙ্কন করেছি যাদের ক্ষেত্রফল সমান। F ও G যথাক্রমে ত্রিভুজদুটির ভরকেন্দ্র হলে প্রমাণ করি যে, FG || QR.
9. প্রমাণ করি যে, কোনো সমদ্বিবাহু ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির যে-কোনো একটির সংলগ্ন কোণ দুটি সমান।
10. ∆ABC এবং ∆DBC একই ভূমি BC-এর উপর এবং BC-এর একই পার্শ্বে অবস্থিত। BC বাহুর উপর E যে-কোনো একটি বিন্দু। E বিন্দু দিয়ে AB এবং BD-এর সমান্তরাল সরলরেখা AC এবং DC বাহুকে যথাক্রমে F ও G বিন্দুতে ছেদ করে। প্রমাণ করি যে, AD || FG.
11. অতিসংক্ষিপ্র উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)
(i) ∆ABC-এর BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে X এবং Y বিন্দুতে ছেদ করে। AX = 2.4 সেমি., AY = 3.2 সেমি. এবং YC = 4.8 সেমি., হলে, AB-এর দৈর্ঘ্য(a) 3.6 সেমি. (b) 6 সেমি. (c) 6.4 সেমি. (d) 7.2 সেমি.
(ii) ∆ABC ত্রিভুজের AB এবং AC বাহুর উপর D ও E বিন্দু এমনভাবে অবস্থিত যে DE || BC এবং AD : DB = 3:1; যদি EA = 3.3 সেমি. হয়, তাহলে AC-এর দৈর্ঘ্য
(a) 1.1 সেমি. (b) 4 সেমি. (c) 4.4 সেমি. (d) 5.5 সেমি.
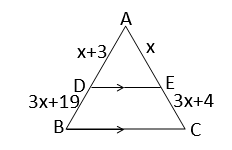
(iii)
পাশের চিত্রে DE || BC হলে, x-এর মান
(a) 4 (b) 1 (c) 3 (d) 2
(iv) ABCD ট্রাপিজিয়ামের AB || DC এবং AD ও BC বাহুর উপর P ও Q বিন্দু দুটি এমনভাবে অবস্থিত যে PQ || DC; যদি PD = 18 সেমি., BQ = 35 সেমি., QC = 15 সেমি. হয়, তাহলে AD-এর দৈর্ঘ্য
(a) 60 সেমি. (b) 30 সেমি. (c) 12 সেমি. (d) 15 সেমি.
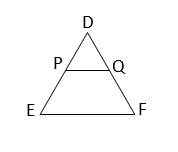
(v)
পাশের চিত্রে, DP = 5 সেমি., DE = 15 সেমি., DQ= 6 সেমি. এবং QF = 18 সেমি. হলে,
(a) PQ = EF (b) PQ|| EF (c) PQ ≠ EF (d) PQ ∦ EF
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি ।
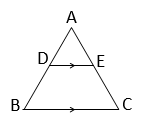
(i) দুটি সদৃশ ত্রিভুজ সর্বদা সর্বসম। (ii)
পাশের চিত্রে DE || BC হলে, \(\frac{AB}{BD}=\frac{AC}{CE}\) হবে।
(C) শূন্যস্থান পূরণ করি।
(i) একটি ত্রিভুজের যে-কোনো বাহুর সমান্তরাল সরলরেখা অপর দুটি বাহুকে বা তাদের বর্ধিতাশংকে ___________ বিভক্ত করে। (ii) দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দুটি সাধারণ হলে ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের ___________ ।
(iii) একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের সমান্তরাল সরলরেখা অপর বাহুদ্বয়কে ___________ বিভক্ত করে।
12. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)
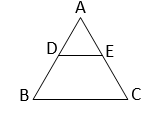
(i) পাশের চিত্রে, ABC ত্রিভুজে \(\frac{AD}{DB}=\frac{AE}{EC}\) এবং ∠ADE = ∠ACB হলে, বাহুভেদে ABC ত্রিভুজটি কী ধরনের লিখি।
(iii)
পাশের চিত্রে DE || BC এবং AD : BD = 3:5 হলে, ∆ADE-এর ক্ষেত্রফল : ∆CDE-এর ক্ষেত্রফল কত তা লিখি।
(iii)
পাশের চিত্রে, LM || AB এবং AL= (x-3) একক, AC = 2x একক, BM = (x-2) একক এবং BC= (2x + 3) একক হলে, x-এর মান নির্ণয় করি।

(iv)
পাশের চিত্রে, ABC ত্রিভুজে DE || PQ || BC এবং AD=3 সেমি., DP = x সেমি., PB = 4 সেমি., AE = 4 সেমি., EQ = 5 সেমি., QC =y সেমি. হলে, x এবং y-এর মান নির্ণয় করি।

(v)
পাশের চিত্রে, DE || BC, BE || XC এবং \(\frac{AD}{DB}=\frac{2}{1}\) হলে, \(\frac{AX}{XB}\) -এর মান নির্ণয় করি।

কষে দেখি 18.3 [উত্তর দেখতে Question এর ওপর Click করুন ]
Top
1. 
2.
3. আমাদের মাঠে 6 সেমি. দৈর্ঘ্যের একটি কাঠির 4 সেমি. দৈর্ঘ্যের ছায়া মাটিতে পড়েছে। ওই একই সময়ে যদি একটি উঁচু টাওয়ারের ছায়ার দৈর্ঘ্য 28 মিটার হয়, তবে টাওয়ারের উচ্চতা কত হবে হিসাব করে লিখি।
4. প্রমাণ করি যে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।
5. তিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A, B, C ও X, Y, Z বিন্দুতে ছেদ করেছে, প্রমাণ করি যে, AB : BC = XY : YZ
6. PQRS একটি ট্রাপিজিয়াম অঙ্কন করেছি যার PQ || SR; PR ও QS কর্ণ দুটি O বিন্দুতে পরস্পরকে ছেদ করলে, প্রমাণ করি যে, OP : OR = OQ : OS; যদি SR = 2PQ হয়, তাহলে প্রমাণ করি যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখণ্ডক বিন্দুর একটি বিন্দু হবে।
7. PQRS একটি সামান্তরিক। S বিন্দুগামী একটি সরলরেখা PQ এবং বর্ধিত RQ-কে যথাক্রমে X ও Y বিন্দুতে ছেদ করলে, প্রমাণ করি যে, PS : PX = QY : QX = RY : RS.
8. দুটি সূক্ষ্মকোণী ত্রিভুজ ∆ABCও ∆PQR সদৃশকোণী। তাদের পরিকেন্দ্র যথাক্রমে X ও Y; BC ও QR অনুরূপ বাহু হলে, প্রমাণ করি যে, BX: QY = BC: QR.
9. কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে। P, S ও R, Q যুক্ত করে, প্রমাণ করি যে, ∆PXS ও ∆RSQ সদৃশকোণী। এর থেকে প্রমাণ করি যে, PX.XQ=RX.XS
অথবা একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।
10. একটি সরলরেখার উপর P এবং Q দুটি বিন্দু। P এবং Q বিন্দুতে সরলরেখাটির উপর যথাক্রমে PR এবং QS লম্ব। PS এবং QR পরস্পরকে O বিন্দুতে ছেদ করে। OT, PQ-এর উপর লম্ব। প্রমাণ করি যে, \(\frac{1}{OT}=\frac{1}{PR}+\frac{1}{QS}\)
11. একটি বৃত্তে অন্তর্লিখিত ∆ABC; বৃত্তের ব্যাস AD এবং AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, ∆AEB এবং ∆ACD সদৃশকোণী। এর থেকে প্রমাণ করি যে, AB.AC=AE.AD.
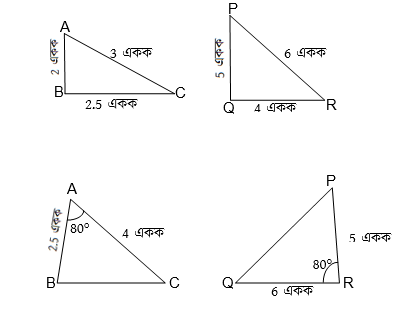
নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লিখি।

2.
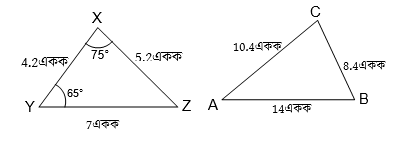
নীচের ত্রিভুজ জোড়া দেখি ও ∠A-এর মান হিসাব করে লিখি।

3. আমাদের মাঠে 6 সেমি. দৈর্ঘ্যের একটি কাঠির 4 সেমি. দৈর্ঘ্যের ছায়া মাটিতে পড়েছে। ওই একই সময়ে যদি একটি উঁচু টাওয়ারের ছায়ার দৈর্ঘ্য 28 মিটার হয়, তবে টাওয়ারের উচ্চতা কত হবে হিসাব করে লিখি।
4. প্রমাণ করি যে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।
5. তিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A, B, C ও X, Y, Z বিন্দুতে ছেদ করেছে, প্রমাণ করি যে, AB : BC = XY : YZ
6. PQRS একটি ট্রাপিজিয়াম অঙ্কন করেছি যার PQ || SR; PR ও QS কর্ণ দুটি O বিন্দুতে পরস্পরকে ছেদ করলে, প্রমাণ করি যে, OP : OR = OQ : OS; যদি SR = 2PQ হয়, তাহলে প্রমাণ করি যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখণ্ডক বিন্দুর একটি বিন্দু হবে।
7. PQRS একটি সামান্তরিক। S বিন্দুগামী একটি সরলরেখা PQ এবং বর্ধিত RQ-কে যথাক্রমে X ও Y বিন্দুতে ছেদ করলে, প্রমাণ করি যে, PS : PX = QY : QX = RY : RS.
8. দুটি সূক্ষ্মকোণী ত্রিভুজ ∆ABCও ∆PQR সদৃশকোণী। তাদের পরিকেন্দ্র যথাক্রমে X ও Y; BC ও QR অনুরূপ বাহু হলে, প্রমাণ করি যে, BX: QY = BC: QR.
9. কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে। P, S ও R, Q যুক্ত করে, প্রমাণ করি যে, ∆PXS ও ∆RSQ সদৃশকোণী। এর থেকে প্রমাণ করি যে, PX.XQ=RX.XS
অথবা একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।
10. একটি সরলরেখার উপর P এবং Q দুটি বিন্দু। P এবং Q বিন্দুতে সরলরেখাটির উপর যথাক্রমে PR এবং QS লম্ব। PS এবং QR পরস্পরকে O বিন্দুতে ছেদ করে। OT, PQ-এর উপর লম্ব। প্রমাণ করি যে, \(\frac{1}{OT}=\frac{1}{PR}+\frac{1}{QS}\)
11. একটি বৃত্তে অন্তর্লিখিত ∆ABC; বৃত্তের ব্যাস AD এবং AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, ∆AEB এবং ∆ACD সদৃশকোণী। এর থেকে প্রমাণ করি যে, AB.AC=AE.AD.
কষে দেখি 18.4 [উত্তর দেখতে Question এর ওপর Click করুন ]
Top
1. ∆ABC-এর \(\angle\)ABC = 90° এবং BD \(\bot\) AC; যদি BD = 8 সেমি. এবং AD = 5 সেমি. হয়, তবে CD-এর দৈর্ঘ্য হিসাব করে লিখি।
2. ABC একটি সমকোণী ত্রিভুজ যার \(\angle\)B সমকোণ এবং BD \(\bot\) AC; যদি AD = 4 সেমি. এবং CD = 16 সেমি. হয়, তবে BD ও AB-এর দৈর্ঘ্য হিসাব করে লিখি।
3. O কেন্দ্রবিশিষ্ট একটি বৃত্তের AB একটি ব্যাস। P বৃত্তের উপর যে-কোনো একটি বিন্দু। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে। যদি বৃত্তের ব্যাসার্ধ r হয়, প্রমাণ করি যে, PQ.PR = r\(^2\)
4. AB-কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করেছি। AB-এর উপর যে-কোনো বিন্দু C থেকে AB-এর উপর লম্ব অঙ্কন করেছি যা অর্ধবৃত্তকে D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, CD, AC ও BC-এর মধ্যসমানুপাতী।
5. সমকোণী ত্রিভুজ ABC-এর \(\angle\)A সমকোণ। অতিভুজ BC-এর উপর লম্ব AD হলে, প্রমাণ করি যে, \(\frac{∆ABC}{∆ACD}=\frac{BC^2}{AC^2} \)
6. O কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ করি যে,
(i) BD\(^2\)=AD.DC
(ii) যে-কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান।
7. অতিসংক্ষিপ্র উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)
(i) ∆ABC ও ∆DEF এ \(\frac{AB}{DE}=\frac{BC}{FD}=\frac{AC}{EF}\) হলে,
(ii) ∆DEF ও ∆PQR-এ \(\angle\)D = \(\angle\)Q এবং \(\angle\)R = \(\angle\)E হলে, নীচের কোনটি সঠিক নয় লিখি।
(iii) ABC ও DEF ত্রিভুজে \(\angle\)A=\(\angle\)E = 40° , AB : ED=AC : EF এবং \(\angle\)F = 65° হলে \(\angle\)B-এর মান
(iv) ∆ABC এবং ∆PQR-এ \(\frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}\) হলে,
(v) ABC ত্রিভুজে AB = 9 সেমি., BC = 6 সেমি. এবং CA = 7.5 সেমি.। DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF; EF = 8 সেমি. এবং ∆DEF ~ ∆ABC হলে ∆DEF-এর পরিসীমা
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি ।
(i) দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ।
(ii)
(iii) ∆PQR-এর QR বাহুর উপর D এমন একটি বিন্দু যে PD\(\bot\)QR; সুতরাং, ∆PQD ~ ∆RPD
(C) শূন্যস্থান পূরণ করি।
(i) দুটি ত্রিভুজ সদৃশ হবে যদি তাদের বাহুগুলি ____________সমানুপাতী হয়।
(ii) ∆ABC ও ∆DEF-এর পরিসীমা যথাক্রমে 30 সেমি. এবং 18 সেমি.। ∆ABC ~ ∆DEF; BC ও EF অনুরূপ বাহু। যদি BC = 9 সেমি. হয়, তাহলে EF =_____________ সেমি.।
8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)
(i) 
(iii)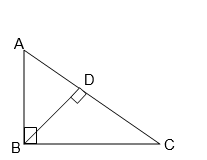
(iii)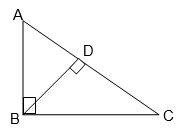
(iv) ABCD ট্রাপিজিয়ামের BC || AD এবং AD = 4 সেমি.। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে \(\frac{AO}{OC}=\frac{DO}{OB}=\frac{1}{2}\) হয়। BC-এর দৈর্ঘ্য কত তা লিখি।
(v) ∆ABC~∆DEF এবং ∆ABC ও ∆DEF -এ AB, BC ও CA বাহুর অনুরূপ বাহুগুলি যথাক্রমে DE, EF ও DF; ∠A = 47° এবং ∠E = 83° হলে, ∠C-এর পরিমাপ কত তা লিখি।
2. ABC একটি সমকোণী ত্রিভুজ যার \(\angle\)B সমকোণ এবং BD \(\bot\) AC; যদি AD = 4 সেমি. এবং CD = 16 সেমি. হয়, তবে BD ও AB-এর দৈর্ঘ্য হিসাব করে লিখি।
3. O কেন্দ্রবিশিষ্ট একটি বৃত্তের AB একটি ব্যাস। P বৃত্তের উপর যে-কোনো একটি বিন্দু। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে। যদি বৃত্তের ব্যাসার্ধ r হয়, প্রমাণ করি যে, PQ.PR = r\(^2\)
4. AB-কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করেছি। AB-এর উপর যে-কোনো বিন্দু C থেকে AB-এর উপর লম্ব অঙ্কন করেছি যা অর্ধবৃত্তকে D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, CD, AC ও BC-এর মধ্যসমানুপাতী।
5. সমকোণী ত্রিভুজ ABC-এর \(\angle\)A সমকোণ। অতিভুজ BC-এর উপর লম্ব AD হলে, প্রমাণ করি যে, \(\frac{∆ABC}{∆ACD}=\frac{BC^2}{AC^2} \)
6. O কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ করি যে,
(i) BD\(^2\)=AD.DC (ii) যে-কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান।
7. অতিসংক্ষিপ্র উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)
(i) ∆ABC ও ∆DEF এ \(\frac{AB}{DE}=\frac{BC}{FD}=\frac{AC}{EF}\) হলে, (a) \(\angle\)B=\(\angle\)E (b) \(\angle\)A=\(\angle\)D (c) \(\angle\)B=\(\angle\)D (d) \(\angle\)A=\(\angle\)F
(ii) ∆DEF ও ∆PQR-এ \(\angle\)D = \(\angle\)Q এবং \(\angle\)R = \(\angle\)E হলে, নীচের কোনটি সঠিক নয় লিখি।
(a) \(\frac{EF}{PR}=\frac{DF}{PQ}\) (b) \(\frac{QR}{PQ}=\frac{EF}{DF}\) (c) \(\frac{DE}{QR}=\frac{DF}{PQ}\) (d) \(\frac{EF}{RP}=\frac{DE}{QR}\)
(iii) ABC ও DEF ত্রিভুজে \(\angle\)A=\(\angle\)E = 40° , AB : ED=AC : EF এবং \(\angle\)F = 65° হলে \(\angle\)B-এর মান
(a) 35° (b) 65° (c) 75° (d) 85°
(iv) ∆ABC এবং ∆PQR-এ \(\frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}\) হলে,
(a) \(\angle\)A=\(\angle\)Q (b) \(\angle\)A=\(\angle\)P (c) \(\angle\)A=\(\angle\)R (d) \(\angle\)B=\(\angle\)Q
(v) ABC ত্রিভুজে AB = 9 সেমি., BC = 6 সেমি. এবং CA = 7.5 সেমি.। DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF; EF = 8 সেমি. এবং ∆DEF ~ ∆ABC হলে ∆DEF-এর পরিসীমা
(a) 22.5 সেমি. (b) 25 সেমি. (c) 27 সেমি. (d) 30 সেমি.
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি ।
(i) দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ। (ii)
পাশের চিত্রে \(\angle\)ADE = \(\angle\)ACB হলে, ∆ADE ~∆ACB

(iii) ∆PQR-এর QR বাহুর উপর D এমন একটি বিন্দু যে PD\(\bot\)QR; সুতরাং, ∆PQD ~ ∆RPD
(C) শূন্যস্থান পূরণ করি।
(i) দুটি ত্রিভুজ সদৃশ হবে যদি তাদের বাহুগুলি ____________সমানুপাতী হয়। (ii) ∆ABC ও ∆DEF-এর পরিসীমা যথাক্রমে 30 সেমি. এবং 18 সেমি.। ∆ABC ~ ∆DEF; BC ও EF অনুরূপ বাহু। যদি BC = 9 সেমি. হয়, তাহলে EF =_____________ সেমি.।
8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A)
(i) পাশের চিত্রে, ∠ACB = ∠BAD এবং AD \(\bot\) BC; AC = 15 সেমি., AB = 20 সেমি. এবং BC = 25 সেমি. হলে, AD-এর দৈর্ঘ্য কত তা লিখি।

(iii)
পাশের চিত্রে, ∠ABC = 90° এবং BD \(\bot\) AC; যদি AB = 30 সেমি., BD = 24 সেমি. এবং AD = 18 সেমি. হলে, BC-এর দৈর্ঘ্য কত তা লিখি।

(iii)
পাশের চিত্রে, ∠ABC = 90° এবং BD \(\bot\) AC; যদি BD = 8 সেমি. এবং AD = 4 সেমি. হয়, তাহলে CD-এর দৈর্ঘ্য কত তা লিখি।

(iv) ABCD ট্রাপিজিয়ামের BC || AD এবং AD = 4 সেমি.। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে \(\frac{AO}{OC}=\frac{DO}{OB}=\frac{1}{2}\) হয়। BC-এর দৈর্ঘ্য কত তা লিখি।
(v) ∆ABC~∆DEF এবং ∆ABC ও ∆DEF -এ AB, BC ও CA বাহুর অনুরূপ বাহুগুলি যথাক্রমে DE, EF ও DF; ∠A = 47° এবং ∠E = 83° হলে, ∠C-এর পরিমাপ কত তা লিখি।
নিজে করি [উত্তর দেখতে Question এর ওপর Click করুন ]
Top
Will be available soon...
মাধ্যমিকের প্রশ্ন [উত্তর দেখতে Question এর ওপর Click করুন ]
Top