θ -এর মান - (a) 30° (b) 45° (c) 60° (d) 75°
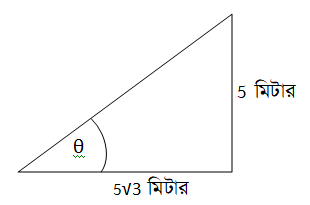
Answer: A
\(\tan\theta=\)লম্ব/ভূমি \(=\cfrac{5}{5\sqrt3}=\cfrac{1}{\sqrt3}=tan 30^o\)
\(\therefore \theta =30^o\)
\(\tan\theta=\)লম্ব/ভূমি \(=\cfrac{5}{5\sqrt3}=\cfrac{1}{\sqrt3}=tan 30^o\)
\(\therefore \theta =30^o\)