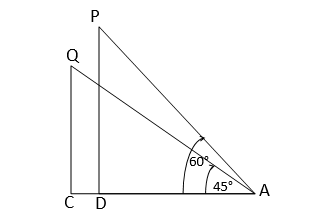
---

ধরি,A বিন্দু থেকে ঘুড়িটি ওড়ানো হচ্ছে । সুতোটি যখন অনুভূমিক রেখার সঙ্গে 60° কোণে থাকে তখন ঘুড়িটির অবস্থান P বিন্দু এবং যখন 45° কোণে থাকে তখন তার অবস্থান Q দুক্ষেত্রে সুতোর দৈর্ঘ্য AP=AQ=250 মিটার।
P এবং Q বিন্দু থেকে ভূমির অপর লম্ব যথাক্রমে PD এবং QC

সমকোণী ত্রিভূজ APD থেকে পাই
sin60°=লম্ব /অতিভূজ \(=\frac{PD}{AP}=\frac{PD}{250}\)
বা,sin60° \(=\frac{PD}{250}\)
বা, \(\cfrac{√3}{2}=\frac{PD}{250}\)
বা, PD \(=\cfrac{250√3}{2}=125√3\)

সমকোণী ত্রিভূজ AQC থেকে পাই
sin45°=(লম্ব )/অতিভূজ \(=\frac{QC}{AQ}=\frac{QC}{250}\)
বা,sin45° \(=\frac{QC}{250}\)
বা, \(\cfrac{1}{√2}=\frac{QC}{250}\)
বা,QC \(=\frac{250}{√2}=\frac{250√2}{2}=125√2\)

∴প্রথম ক্ষেত্রে ঘুড়িটি \(125√3\) মিটার এবং দ্বিতীয় ক্ষেত্রে ঘুড়িটি\( 125√2\) মিটার উচ্চতায় উড়বে ।
আবার যেহেতু \(125√3>125√2\),তাই প্রথম ক্ষেত্রে ঘুড়িটি বেশি উচ্চতায় উড়বে ।