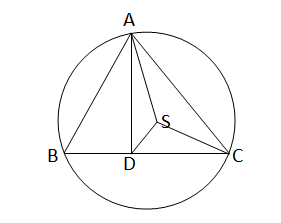
---

ধরি,∆ABC এর পরিবৃত্তের কেন্দ্র S,এবং AD,BC বাহুর ওপর লম্ব।
প্রমান করতে হবে যে,\(\angle\)BAD=\(\angle\)SAC

অঙ্কনঃ S,A এবং S,C যোগ করা হল।

প্রমানঃ ∆ABD এর
\(\angle\)ABD=180°-(\(\angle\)BDA+\(\angle\)BAD)
=180°-(90°+\(\angle\)BAD)=90°-\(\angle\)BAD
অর্থাৎ,\(\angle\)ABC=90°-\(\angle\)BAD---(i)

আবার,AC চাপের ওপর কেন্দ্রস্থ কোণ \(\angle\)ASC এবং বৃত্তস্থ কোণ \(\angle\)ABC
∴\(\angle\)ASC=2\(\angle\)ABC
বা,\(\angle\)ASC=2(90°-\(\angle\)BAD)--(ii) [(i)নং সমীকরনের মান বসিয়ে]

∆ASC এর AS=SC=বৃত্তের ব্যাসার্ধ
∴\(\angle\)SAC=\(\angle\)ACS
∴\(\angle\)ASC= 180°-(\(\angle\)SAC+\(\angle\)ACS)=180°-2\(\angle\)SAC---(iii)

(ii)এবং (iii)নং সমীকরন থেকে পাই,
2(90°-\(\angle\)BAD)= 180°-2\(\angle\)SAC
বা,180°-2\(\angle\)BAD=180°-2\(\angle\)SAC
∴\(\angle\)BAD=\(\angle\)SAC (প্রমানিত)