নিবেদিতাদের ক্লাসের 35 জন শিক্ষার্থীর ওজনের তথ্য হলো,
| ওজন(কিগ্রা) | 38-এর কম | 40-এর কম | 42-এর কম |
| শিক্ষার্থীর সংখ্যা | 0 | 4 | 6 |
| 44-এর কম | 46-এর কম | 48-এর কম | 50-এর কম | 52-এর কম |
| 9 | 12 | 28 | 32 | 35 |
x অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য =1 একক এবং y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য=1 একক ধরে (38,0), (40,4), (42,6), (44,9), (46,12), (48,28), (50,32 ), (52,35) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ক্ষুদ্রতর সূচক ওজাইভ পাওয়া গেল।
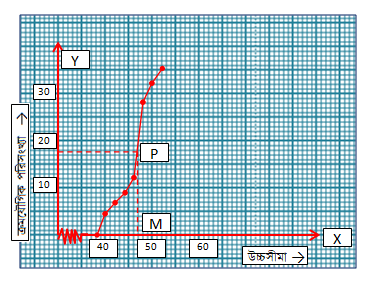
এখানে মোট শিক্ষার্থী(n)= 35 জন।
\(∴ \cfrac{n}{2}=17.5\)
(0,17.5)বিন্দু দিয়ে x অক্ষের সমান্তরাল সরলরেখা ওজাইভকে P বিন্দুতে ছেদ করল। P বিন্দু দিয়ে OX এর ওপর PM লম্ব টানলে তা x অক্ষকে M বিন্দুতে ছেদ করে। M বিন্দুর স্থানাঙ্ক (46.69)
∴মধ্যমা= 46.69
সূত্রের সাহায্যে মধ্যমা নির্ণয়
| শ্রেণি-সীমানা | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক) |
|---|---|---|
| 0-38 | 0 | 0 |
| 38-40 | 4 | 4 |
| 40-42 | 2 | 6 |
| 42-44 | 3 | 9 |
| 44-46 | 3 | 12 |
| 46-48 | 16 | 28 |
| 48-50 | 4 | 32 |
| 50-52 | 3 | 35=n |
সুতরাং মধ্যমা শ্রেণিটি হল (46-48)
∴সূত্রের সাহায্যে মধ্যমা \(=l+\left[\cfrac{\cfrac{n}{2}-cf}{f}\right]×h\) [ এখানে, \(l=46,n=35, cf=12,f=16,h=2\)]
\(=46+\left[\cfrac{17.5-12}{16}\right]×2\)
\(=46+\cfrac{5.5}{16}×2\)
\(=46+\cfrac{11}{16}\)
\(=46+0.69=46.69\) (প্রায়)