একটি লাইট হাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুলের গোড়ার অবনতি কোণ যদি যথাক্রমে 60° ও 30° হয় এবং কাছের জাহাজের মাস্তুল যদি লাইট হাউস থেকে 150 মিটার দূরত্বে থাকে, তাহলে দূরের জাহাজের মাস্তুল লাইটি হাউস থেকে কত দূরত্বে রয়েছে এবং লাইট হাউসটির উচ্চতা হিসাব করে লিখি।
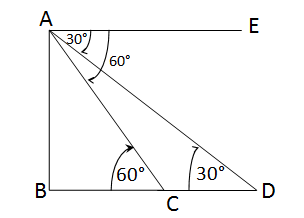
ধরি,AB লাইট হাউস,A বিন্দু থেকে লাইট হাউস থেকে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুল C এবং D বিন্দুর অবনতি কোণ যথাক্রমে 60° এবং 30°
∴∠EAC=60°
এবং ∠EAD=30° [ধরি,AE||BD]
BC=কাছের জাহাজের দূরত্ব=150 মিটার এবং
∠ADB=∠EAD=30° ও ∠ACB=∠EAC =60°
সমকোণী ত্রিভূজ ABC থেকে পাই
\(tan60°=\cfrac{AB}{BC}=\cfrac{AB}{150}\)
বা, \(tan60°= \cfrac{AB}{150}\)
বা,\(√3=\cfrac{AB}{150}\)
বা, \(AB=150√3\)
সমকোণী ত্রিভূজ ABD থেকে পাই
\(tan30°= \cfrac{AB}{BD}=\cfrac{150√3}{BD}\)
বা, \(tan30°=\cfrac{150√3}{BD}\)
বা, \(\cfrac{1}{√3}=\cfrac{150√3}{BD}\)
বা, \(BD=150\sqrt3×\sqrt3=450\)
∴ দূরের জাহাজের মাস্তুল লাইট হাউস থেকে BD=450 মিটার দূরত্বে রয়েছে । এবং চিমনির উচ্চতা AB=150√3 মিটার ।