একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ, প্রমাণ করো। Madhyamik 2016 , 2013 , 2010 , 2007
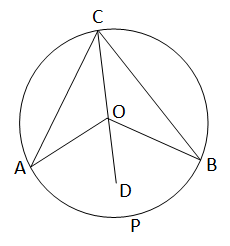
মনে করি O কেন্দ্রীয় বৃত্তের বৃত্তচাপ APB এর দ্বারা গঠিত কেন্দ্রস্থ কোণ \(\angle\)AOB এবং একটি বৃত্তস্থ কোণ \(\angle\)ACB
প্রমান করতে হবে যে, \(\angle\)AOB=\(\angle\)ACB
অঙ্কন : C,O যুক্ত করে D বিন্দু পর্যন্ত বর্ধিত করা হল ।
প্রমান : \(\triangle\)AOC এর
OA=OC [একই বৃত্তের ব্যাসার্ধ ]
\(\therefore \angle\)OCA=\(\angle\)OAC
আবার \(\triangle\)AOC এর CO বাহুকে D পর্যন্ত বর্ধিত করায়
বহিঃস্থ \(\angle\)AOD=\(\angle\)OAC+\(\angle\)OCA
=2\(\angle\)OCA \(------(i)\) [\(\because\) \(\angle\)OAC=\(\angle\)OCA]
এখন, \(\triangle\)BOC এর, OB=OC [একই বৃত্তের ব্যাসার্ধ]
সুতরাং, \(\angle\)OBC=\(\angle\)OCB
আবার, \(\triangle\)BOC এর CO বাহুকে D বিন্দু পর্যন্ত বর্ধিত করায়
বহিঃস্থ \(\angle\)BOD=\(\angle\)OCB+\(\angle\)OBC
=2\(\angle\)OCB \(------(ii)\) [\(\because \angle\)OBC=\(\angle\)OCB]
\((i)\) ও \((ii)\) নং সমীকরন থেকে পাই,
\(\angle\)AOD+\(\angle\)BOD=2\(\angle\)OCA+2\(\angle\)OCB
\(\therefore \angle\)AOB=2(\(\angle\)OCA+\(\angle\)OCB)=2\(\angle\)ACB [প্রমাণিত]