প্রমাণ করো যে, যদি দুটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে, তাহলে স্পর্শ বিন্দুটি কেন্দ্র দুটির সংযোজক সরলরেখাশের উপর অবস্থিত হবে । Madhyamik 2019
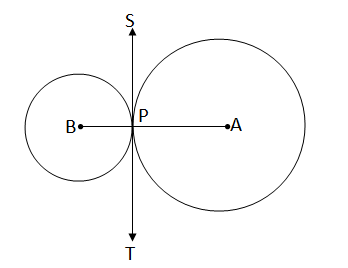
প্রদত্ত : A ও B কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে P বিন্দুতে স্পর্শ করেছে । প্রমান করতে হবে: A, P ও B সমরেখ ।
অঙ্কন: A,P ও B,P যোগ করলাম।
প্রমান: A কেন্দ্রীয় ও B কেন্দ্রীয় বৃত্তদুটি পরস্পরকে P বিন্দুতে স্পর্শ করেছে। ∴ P বিন্দুতে বৃত্তদুটির একটি সাধারণ স্পর্শক আছে।
ধরি, ST হলো সাধারণ স্পর্শক যা দুটি বৃত্তকেই P বিন্দুতে স্পর্শ করেছে ।
∵ A কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং AP স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ AP⊥ST
আবার, যেহেতু B কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং BP স্পর্শবিন্দুগামী ব্যাসার্ধ,
∴ BP⊥ST
∴ AP ও BP একই P বিন্দুতে ST সরলরেখার উপর লম্ব।
∴ AP ও BP একই সরলরেখায় অবস্থিত অর্থাৎ A,P ও B সমরেখ। (প্রমাণিত)