একটি পাঁচতলা বাড়ির ছাদের কোনো বিন্দু থেকে দেখলে মনুমেন্টের চূড়ার উন্নতি কোণ ও গোড়ার অবনতি কোণ যথাক্রমে 60° ও 30°; বাড়িটির উচ্চতা 16 মিটার হলে, মনুমেন্টের উচ্চতা এবং বাড়িটি মনুমেন্ট থেকে কত দূরে অবস্থিত হিসাব করে লিখি।
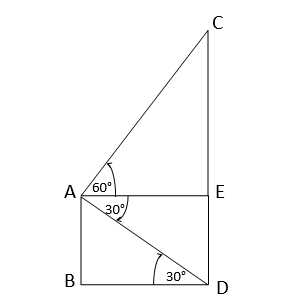
মনে করি,AB একটি পাঁচতলা বাড়ি,যার ছাদ A বিন্দু থেকে মনুমেন্টের চূড়া C বিন্দুর উন্নতি কোণ এবং গোড়া D বিন্দুর অবনতি কোণ যথাক্রমে 60° এবং 30°;বাড়ির উচ্চতা AB=16 মিটার ।
∴∠CAE=60°[ধরি AE||BD]
∠EAD=30°
∴∠ADB=∠EAD=30°
সমকোণী ত্রিভূজ ABD থেকে পাই
\(tan30°= \cfrac{AB}{BD}=\cfrac{16}{BD}\)
বা, \(tan30°= \cfrac{16}{BD}\)
বা, \(\cfrac{1}{√3}=\cfrac{16}{BD}\)
বা, \(BD =16√3\)
\(∴AE=BD=16√3\)
সমকোণী ত্রিভূজ AEC থেকে পাই
\(tan60°= \cfrac{CE}{AE}=\cfrac{CE}{16√3}\)
বা, \(tan60°=\cfrac{CE}{16√3}\)
বা, \(√3=\cfrac{CE}{16√3}\)
বা, \(CE=16√3×3=48\)
∴CD=CE+ED=CE+AB=48+16 =64
∴মনুমেন্টের উচ্চতা=64 মিটার এবং বাড়িটি থেকে মনুমেন্টের দূরত্ব BD=16√3 মিটার ।