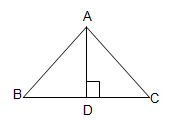
---

∆ABD এবং ∆ADC এর মধ্যে
∠BAD=∠ACD (প্রদত্ত)
∠ADB=∠ADC(উভয়েই সমকোণ)
অবশিষ্ট ∠ABD=∠CAD
∴∆ABD~∆ADC

\(∴\frac{BD}{AD}=\frac{AB}{AC}=\frac{AD}{DC}\)
বা, \(\frac{BD}{AD}=\frac{AB}{AC}\)
বা,\(\frac{BD}{AD}=\frac{20}{15}=\frac{4}{3}---(i)\)

আবার, \(\frac{AB}{AC}=\frac{AD}{DC}\)
বা, \(\frac{20}{15}=\frac{AD}{DC}\)
বা, \(\frac{DC}{AD}=\frac{15}{20}=\frac{3}{4}---(ii)\)

\((i)\) এবং \((ii)\) যোগ করে পাই,
\(\frac{BD}{AD}+\frac{DC}{AD}=\frac{4}{3}+\frac{3}{4}\)
বা,\(\frac{BD+DC}{AD}=\frac{16+9}{12}\)
বা, \(\frac{BC}{AD}=\frac{25}{12}\)
বা, \(\frac{25}{AD}=\frac{25}{12}\)
∴AD=12

∴AD এর দৈর্ঘ্য 12 সেমি ।