11 মিটার উঁচু একটি বাড়ির ছাদ থেকে দেখলে একটি ল্যাম্পপোস্টের চূড়া ও পাদবিন্দুর অবনতি কোণ হয় যথাক্রমে 30° এবং 60°। ল্যাম্পপোস্টের উচ্চতা নির্ণয় করো।
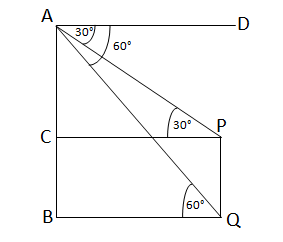
ধরি,AB=11 মিটার উঁচু একটি বাড়ির ছাদ A বিন্দু থেকে দেখলে একটি ল্যাম্পপোস্ট PQ এর চূড়া P এবং পাদদেশ Q বিন্দুর অবনতি কোণ যথাক্রমে 30° ও 60°
∴∠DAP=30° ও ∠DAQ=60° [ ধরি,AD∥BQ]
CP∥BQ অঙ্কন করা হল।
∠APC=একান্তর ∠DAP=30° এবং
∠AQB=একান্তর ∠DAQ=60°
সমকোণী ত্রিভূজ ∆ABQ থেকে পাই,
\(tan60°= \cfrac{AB}{BQ}\)
বা, \(√3=\cfrac{AB}{BQ}\)
বা, \(BQ=\cfrac{AB}{√3}=\cfrac{11}{√3}\)
আবার সমকোণী ত্রিভূজ ∆ACP থেকে পাই,
\(tan30°=\cfrac{AC}{CP}\)
বা, \(\cfrac{1}{√3}=\cfrac{AC}{CP}\)
বা, \(AC=\cfrac{CP}{√3}=\cfrac{\cfrac{11}{√3}}{√3}=\cfrac{11}{3}\)
∴ল্যাম্পপোস্টের উচ্চতা\(=PQ=BC\)
\(=AB-AC\)
\(=(11-\cfrac{11}{3})\) মিটার \(\cfrac{33-11}{3}\) মিটার \(=\cfrac{22}{3}\) মিটার \(=7\cfrac{1}{3}\) মিটার