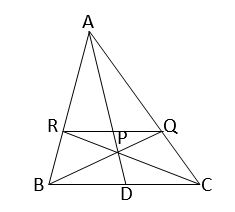
---

\(∆ABC\) এর \(AD\) মধ্যমার উপর \(P \) একটি বিন্দু। বর্ধিত \(BP \) এবং \(CP \) যথাক্রমে \(AC\) ও \(AB \) কে \(Q \) এবং \( R \) বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, \(RQ∥BC\)

অঙ্কনঃ \(R,Q \) যোগ করা হল।

প্রমানঃ \(∆ABC\) এর মধ্যমা \(AD\)
\(∴ ∆ABD=∆ADC\)
আবার, \(∆BPC\) এর মধ্যমা \(PD\)
\(∴ ∆BPD=∆CPD\)

\(∴ ∆ABD-∆BPD=∆ADC-∆CPD\)
অর্থাৎ, \(∆APB=∆APC\)

আবার যেহেতু \(P\) বিন্দু মধ্যমার ওপর অবস্থিত \(∴ ∆ARP=∆APQ\)

\(∴ ∆APB-∆ARP=∆APC-∆APQ\)
সুতরাং, \(∆BRP=∆QPC\)

\(∴ \cfrac{∆ARP}{∆BRP}=\cfrac{∆AQP}{∆CQP}\) অর্থাৎ, \(\cfrac{AR}{BR}=\cfrac{AQ}{QC}\)
\(∴ RQ∥BC\) (প্রমানিত)