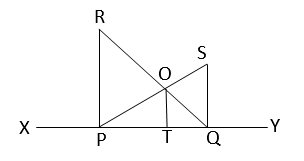
---

\(XY\) সরলরেখার ওপর \(P\) ও \(Q\) দুটি বিন্দু। \(P\) এবং \(Q\) বিন্দুতে অঙ্কিত লম্ব যথাক্রমে \(PR\) ও \(QS; PS\) এবং \(QR\) পরস্পরকে \( O\) বিন্দুতে ছেদ করেছে। \(OT, PQ\) এর ওপর লম্ব।
প্রমান করতে হবে যে, \(\cfrac{1}{OT}=\cfrac{1}{PR}+\cfrac{1}{QS}\)

প্রমানঃ \(∆PQR\) এর
\(PR∥TO\) [ \(∵PR\) ও \(OT \) উভয়েই লম্ব]
\(∴ \cfrac{OT}{PR}=\cfrac{TQ}{PQ}\)
বা, \(PQ=\cfrac{PR.TQ}{OT}---(i)\)

আবার, \(∆PQS\) এর
\(SQ∥OT\) [ \(∵SQ\) ও \(OT\) উভয়েই লম্ব]
\(∴ \cfrac{OT}{QS}=\cfrac{PT}{PQ}\)
বা, \(PQ= \cfrac{PT.QS}{OT}---(ii)\)

\(∴(i)\) এবং \((ii)\) নং থেকে পাই,
\(\cfrac{PR.TQ}{OT}= \cfrac{PT.QS}{OT} \)
বা, \(PR.TQ=PT.QS\)
বা, \(PR.TQ=(PQ-TQ).QS\)
বা, \(PR.TQ=PQ.QS-TQ.QS\)
বা, \(PQ.QS=TQ.QS+PR.TQ \)
বা, \(PQ=\cfrac{TQ.QS+PR.TQ}{QS}---(iii) \)

\((i)\) ও \((iii)\) নং থেকে পাই,
\(\cfrac{PR.TQ}{OT}=\cfrac{TQ.QS+PR.TQ}{QS} \)
বা, \(\cfrac{1}{OT}= \cfrac{TQ.QS+PR.TQ}{QS.PR.TQ} \)
বা, \(\cfrac{1}{OT}=\cfrac{1}{PR}+\cfrac{1}{QS}\) (প্রমানিত)