∆ABC-এর \(\angle\)ABC = 90° এবং BD \(\bot\) AC; যদি BD = 8 সেমি. এবং AD = 5 সেমি. হয়, তবে CD-এর দৈর্ঘ্য হিসাব করে লিখি।
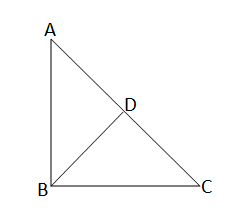
সমকোণী ∆ABD এর AB\(^2\)=AD\(^2\)+BD\(^2\)
বা,AB\(^2\)=5\(^2\)+8\(^2\)=25+64=89
∴AB=\(\sqrt{89}\)
∆ABC এবং ∆ABD দুটি সমকোণী ত্রিভূজের AB সাধারন এবং AB সংলগ্নকোণ \(\angle\)CAB সাধারণ
∴∆ABC ও ∆ABD সদৃশ
∴ \(\cfrac{AB}{AC}=\cfrac{AD}{AB}\)
বা,AB\(^2\)=AD×AC
বা, \((\sqrt{89})^2\)=5×AC
বা, AC=\(\cfrac{89}{5}\)
∴CD=AC-AD=\(\cfrac{89}{5}-5\)
\(=\cfrac{89-25}{5}=\cfrac{64}{5}=12.8\) সেমি (Answer)