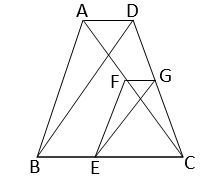
---

\(∆ABC\) এবং \(∆DBC\) একই ভূমি \(BC\) এর উপর এবং \(BC\) এর একই পার্শ্বে অবস্থিত। \(BC\) বাহুর উপর \(E\) যেকোনো একটি বিন্দু। \(E\) বিন্দু দিয়ে \(AB\) এবং \(BD\) এর সমান্তরাল সরলরেখা \(AC\) এবং \(DC\) বাহুকে যথাক্রমে \(F\) ও \(G\) বিন্দুতে ছেদ করে।
প্রমান করতে হবে যে, \(AD∥FG\)

অঙ্কনঃ \(A, D\) যুক্ত করা হল।

প্রমানঃ \(∆ABC\) এর \(BA∥EF\)
\(∴ \cfrac{BE}{EC}= \cfrac{AF}{FC}---(i)\)
আবার \(∆DBC\) এর \(BD∥EG\)
\(∴ \cfrac{BE}{EC}= \cfrac{DG}{GC}---(ii)\)

\(∴(i)\) এবং \( (ii)\) নং সমীকরন থেকে পাই,
\( \cfrac{AF}{FC}= \cfrac{DG}{GC}\)

এখন \(∆ACD\) এর
\( \cfrac{AF}{FC}= \cfrac{DG}{GC} \)
\(∴ AD∥FG \) (প্রমানিত)