ABC একটি সমবাহু ত্রিভুজ এবং AD⊥BC হলে, AD\(^2\) = (a) \(\cfrac{3}{2 DC^2}\) (b) \(2DC^2\) (c) \(3DC^2\) (d) \(4DC^2\)
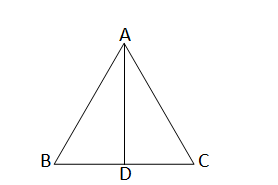
Answer: C
AD\(^2\)=AC\(^2\)-DC\(^2\)
=(2DC)\(^2\)-DC\(^2\) [∵AB=BC=2DC]
=4DC\(^2\)-DC\(^2\)=3DC\(^2\)
AD\(^2\)=AC\(^2\)-DC\(^2\)
=(2DC)\(^2\)-DC\(^2\) [∵AB=BC=2DC]
=4DC\(^2\)-DC\(^2\)=3DC\(^2\)