দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে G ও H বিন্দুতে ছেদ করেছে। এবার G বিন্দুগামী একটি সরলরেখা অঙ্কন করলাম যেটি বৃত্ত দুটিকে P ও Q বিন্দুতে এবং H বিন্দুগামী PQ-এর সমান্তরাল অপর একটি সরলরেখা অঙ্কন করলাম যা বৃত্তদুটিকে R ও S বিন্দুতে ছেদ করল। প্রমাণ করি যে PQ = RS।
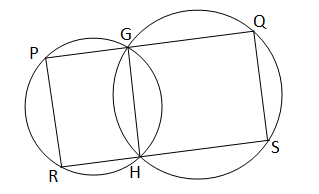
দুটি বৃত্ত পরস্পরকে G এবং H বিন্দুতে ছেদ করেছে। G বিন্দু দিয়ে অঙ্কিত সরলরেখা বৃত্তদুটিকে যথাক্রমে Pএবং Q বিন্দুতে ছেদ করে। H বিন্দু দিয়ে PQ এর সমান্তরাল সরলরেখা বৃত্ত দুটিকে R এবং S বিন্দুতে ছেদ করে।
প্রমান করতে হবে যে,PQ=RS
অঙ্কনঃ P,R;G,H এবং Q,S যুক্ত করা হল ।
প্রমানঃ বৃত্তস্থ SHGQ চতুর্ভূজের
\(\angle\)QSH+\(\angle\)HGQ=2 সমকোণ
আবার,PQ সরলরেখার ওপর G বিন্দুতে GH দন্ডায়মান
∴\(\angle\)HGQ+\(\angle\)HGP=2 সমকোণ
∴\(\angle\)QSH+\(\angle\)HGQ=\(\angle\)HGQ+\(\angle\)HGP
অর্থাৎ,\(\angle\)QSH=\(\angle\)HGP---(i)
বৃত্তস্থ PRHG চতুর্ভূজের
\(\angle\)PRH+\(\angle\)HGP=2 সমকোণ
বা,\(\angle\)PRH+\(\angle\)QSH=2 সমকোণ [(i) নং সমীকরনের মান বসিয়ে]
যেহেতু,PR এবং QS সরলরেখা দুটিকে RS ভেদ করায় ভেদকের এক পার্শ্বস্থ কোণদুটির সমষ্টি 2 সমকোণ,তাই PR∥QS
এখন PRSQ চতুর্ভূজের PQ∥RS এবং PR∥QS
∴PRSQ একটি সামন্তরিক ।
∴PQ=RS [প্রমানিত]