একটি বৃত্তের উপর তিনটি বিন্দু P, Qও R অবস্থিত। PQও PR-এর উপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, RQ = ST
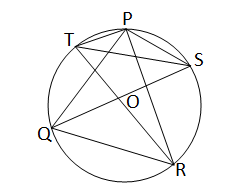
ধরি,P,Q এবং R বৃত্তের ওপর অবস্থিত তিনটি বিন্দু। PQ এবং PR এর ওপর P বিন্দুতে অঙ্কিত লম্বদুটি বৃত্তকে যথাক্রমে S এবং T বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,RQ=ST
অঙ্কনঃ S,Q;T,R;S,T এবং R,Q যুক্ত করা হল।
প্রমানঃ যেহেতু বৃত্তস্থ কোণ \(\angle\)QPS এবং \(\angle\)TPR
উভয়েই সমকোণ,তাই QS এবং TR বৃত্তের ব্যাস ।
এবং QS ও TR এর ছেদবিন্দু O,বৃত্তের কেন্দ্র ।
এখন ∆OQR এবং ∆OTS এর মধ্যে
OR=OT;OS=OQ [বৃত্তের ব্যাসার্ধ]
এবং \(\angle\)QOR=বিপ্রতীপ\(\angle\)TOS
∴∆OQR≅∆OTS
∴RQ=ST (অনুরূপ বাহু)[প্রমানিত]