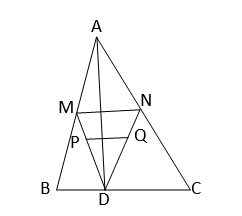
---

ধরি, \(∆ABC\) বাহুর উপর \(D\) একটি বিন্দু। \(P,Q\) যথাক্রমে \(∆ABD\) এবং \(∆ADC\) এর ভরকেন্দ্র ।
প্রমান করতে হবে যে, \(PQ∥BC \)

অঙ্কনঃ \(D,P\) এবং \(D,Q\) যুক্ত করে বর্ধিত করা হল যা যথাক্রমে \(AB\) কে \(M\) এবং \(AC\) কে \(N\) বিন্দুতে ছেদ করে।

প্রমানঃ যেহেতু \(P, ∆ABD\) এর ভরকেন্দ্র
\(∴DM, ∆ABD\) এর একটি মধ্যমা।
\(∴M,AB\) এর মধ্যবিন্দু।

আবার,যেহেতু \(Q, ∆ADC\) এর ভরকেন্দ্র
\(∴ DQ, ∆ADC\) এর একটি মধ্যমা।
\(∴ N, AC \) এর মধ্যবিন্দু।

\(∴ ∆ABC\) এর \(AB\) এবং \(AC\) বাহুর মধ্যমা যথাক্রমে \(M\) এবং \(N\) ; সুতরাং, \(MN∥BC\)

যেহেতু \(DM\) মধ্যমার ওপর \(P, ∆ABD\) এর ভরকেন্দ্র
\(∴ \cfrac{DP}{PM}= \cfrac{2}{1}\)
এবং \(DN\) মধ্যমার ওপর \(Q, ∆ADC\) এর ভরকেন্দ্র
\(∴ \cfrac{DQ}{QN}= \cfrac{2}{1} \)

এখন \(∆MND\) থেকে পাই
\( \cfrac{DP}{PM}= \cfrac{2}{1}= \cfrac{DQ}{QN}\)
বা,\( \cfrac{DP}{PM}= \cfrac{DQ}{QN}\)
\(∴PQ∥MN\)

আবার,যেহেতু, \(MN∥BC\) এবং \(PQ∥MN\)
\(∴ PQ∥MN\) (প্রমানিত)