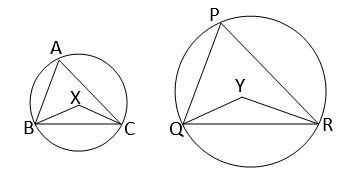
---

∆ABC এবং ∆PQR দুটি সদৃশকোণী ত্রিভূজ,যাদের পরিকেন্দ্র যথাক্রমে X এবং Y;BC এবং QR অনুরূপ বাহু হলে প্রমান করতে হবে যে,BX:QY=BC:QR

অঙ্কনঃ B,X;CX এবং Q,Y;R,Y যুক্ত করা হল।

প্রমানঃ∵∆ABC এবং ∆PQR সদৃশকোণী
∴তাদের বাহুগুলি সমানুপাতী এবং তাদের পরিব্যাসার্ধও সমানুপাতী হবে।
∴ \(\frac{AB}{PQ}=\frac{BC}{QR}=\frac{QC}{PR}=\frac{BX}{QY}\)
অর্থাৎ, \(\frac{BX}{QY}=\frac{BC}{QR}\)
বা,BX:QY=BC:QR (প্রমানিত)