150 মি. লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে। ঘুড়িটি যদি অনুভূমিক রেখার সঙ্গে 60° কোণ করে উড়তে থাকে, তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে হিসাব করে লিখি।
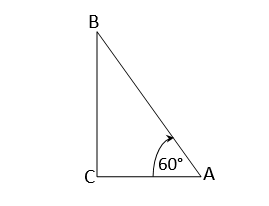
মনে,করি A বিন্দু থেকে ঘুড়িটি ওড়ানো হচ্ছে যা B বিন্দুতে রয়েছে । তাই,AB=সুতোর দৈর্ঘ্য=150 মিটার। এবং B বিন্দু থেকে ভূমির ওপর লম্ব BC=ঘুড়িটির উচ্চতা। আর অনুভূমিক রেখার সঙ্গে ঘুড়িটির উৎপন্ন কোণ ∠BAC=60°
এখন উৎপন্ন সমকোণী ত্রিভূজ ABC থেকে ∠BAC এর পরিপ্রেক্ষিতে পাই
sin∠BAC=লম্ব/অতিভূজ \(=\frac{BC}{AB}=\frac{BC}{150}\)
বা,sin 60° \(=\frac{150}{AB}\)
বা, \(\frac{√3}{2}=\frac{BC}{150}\)
বা,BC \(=\frac{150\times √3}{2}=75√3\)
∴ঘুড়িটি মাঠ থেকে 75√3 মিটার উঁচুতে রয়েছে ।