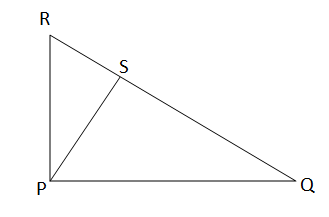
---

প্রদত্তঃ PQR সমকোণী ত্রিভূজের \(\angle P=90 ^o\) এবং \(PS\) , অতিভূজ \(QR\) - এর ওপর লম্ব ।

প্রমান করতে হবে যে, \(\cfrac{1}{PS^2}-\cfrac{1}{PQ^2}=\cfrac{1}{PR^2}\) ।

প্রমানঃ যেহেতু, \( \triangle PSR\) ও \(\triangle PQS\) সদৃশকোণী
\(\therefore \cfrac{PS}{RS}=\cfrac{QS}{PS}\)
বা, \(PS^2=RS\cdot QS -----(i)\)

আবার, \( \triangle PQR\) ও \(\triangle PQS\) সদৃশকোণী
\(\therefore \cfrac{PQ}{QS}=\cfrac{QR}{PQ}\)
বা, \(PQ^2=QS\cdot QR -----(ii)\)

এবং, \(\triangle PQR\) ও \(\triangle PRS\) সদৃশকোণী
\(\therefore \cfrac{PR}{QR}=\cfrac{RS}{PR}\)
বা, \(PR^2=RS\cdot QR -----(iii)\)

বামপক্ষ \(=\cfrac{1}{PS^2}-\cfrac{1}{PQ^2}\)
\(=\cfrac{1}{RS.QS}-\cfrac{1}{QS.QR} \) \([(i) \) এবং \((ii)\) নং সমীকরন থেকে \(]\)
\(=\cfrac{QR-RS}{RS.QS.QR}\)
\(=\cfrac{QS}{ RS.QS.QR}\)
\(=\cfrac{1}{ RS.QR}\)
\(=\cfrac{1}{PR^2}\) [\((iii)\) নং সমীকরনের মান বসিয়ে পাই]
\(=\) ডানপক্ষ [প্রমাণিত]