একটি বৃত্তের বহিঃস্থ কোনো বিন্দু A থেকে অঙ্কিত AB ও AC দুটি স্পর্শক বৃত্তকে B ও C বিন্দুতে স্পর্শ করে। উপচাপ BC-এর উপর অবস্থিত X বিন্দুতে অঙ্কিত স্পর্শক AB ও AC-কে যথাক্রমে D ও E বিন্দুতে ছেদ করে। প্রমাণ করি যে, ∆ADE-এর পরিসীমা = 2 AB.
Loading content...
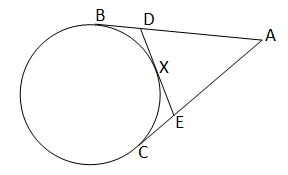
বৃত্তের বহিঃস্থ একটি বিন্দু A থেকে বৃত্তের ওপর AB এবং AC দুটি স্পর্শক। BC উপচাপের ওপর X একটি বিন্দু। X বিন্দু দিয়ে অঙ্কিত বৃত্তের স্পর্শক AB এবন AC কে যথাক্রমে D এবং E বিন্দুতে ছেদ করে।
প্রমান করতে হবে ∆ADE এর পরিসীমা=2AB
প্রমানঃ যেহেতু D বিন্দু থেকে বৃত্তটির ওপর অঙ্কিত স্পর্শক দুটি BD এবং DX এবং E বিন্দু থেকে অঙ্কিত স্পর্শক দুটি EX ও EC
∴BD=DX এবং EC=EX
আবার A থেকে বৃত্তের ওপর AB এবং AC দুটি স্পর্শক
∴AB=AC
এখন,∆ADE এর পরিসীমা=AD+DE+EA
=(AB-BD)+DE+(AC-EC)
=AB+AC+DE-(BD+EC)
=AB+AC+DE-(DX+ EX)
=AB+AC+DE-DE [∵BD=DX এবং EC=EX]
=AB+AC
=2AB [∵AB=AC]
∴∆ADE এর পরিসীমা=2AB(প্রমানিত)
