প্রমাণ করি যে একটি সুষম পঞ্চভুজের যে-কোনো চারটি শীর্ষবিন্দু সমবৃত্তস্থ।
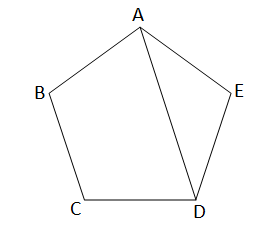
ABCDE একটি সুষম পঞ্চভূজ । প্রমান করতে হবে যে,এর চারটি বিন্দু সমবৃত্তস্থ।
অঙ্কনঃ A,D যুক্ত করা হল।
প্রমানঃ সুষম পঞ্চভূজের প্রতিটি কোনের মান
\(\frac{(2×5-4)×90°}{5} = \frac{540°}{5}\) =108°
এবং প্রতিটি বাহু সমান,অর্থাৎ,
AB=BC=CD=DE=EA
এখন ∆ADE এর DE=EA
∴\(\angle\)EAD=\(\angle\)EDA=\(\frac{180°-108°}{2}\)=36°
সুতরাং,\(\angle\)BAD=108°-36°=72°
∴\(\angle\)BCD+\(\angle\)BAD=108°+72°=180°
∵চতর্ভূজের বিপরীত কোণদ্বয়ের সমষ্টি 180°
∴ABCD চতুর্ভূজটি সমবৃত্তস্থ।
সুতরাং,একটি সুষম পঞ্চভূজের যেকোনো চারটি বিন্দু সমবৃত্তস্থ। (প্রমানিত)