প্রমাণ করো যে বৃত্তের বহিস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিস্থ বিন্দুর সংযোজক রেখাংশ দুটির দৈর্ঘ্য সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে। Madhyamik 2024
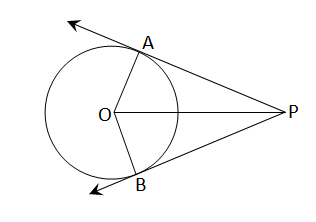
প্রদত্ত: O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে PA ও PB দুটি স্পর্শক যাদের স্পর্শবিন্দু যথাক্রমে A ও B, O,A; O,B; O,P যুক্ত করায় PA ও PB সরলরেখাংশদুটি কেন্দ্রে যথাক্রমে \(\angle\)POA ও \(\angle\)POB দুটি কোণ উৎপন্ন করেছে ।
প্রমান করতে হবে: (i) PA=PB (ii) \(\angle\)POA=\(\angle\)POB
প্রমান: PA ও PB স্পর্শক এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ ।
∴ OA⊥PA এবং OB⊥PB
POA ও POB সমকোণী ত্রিভূজদ্বয়ের মধ্যে,
\(\angle\)OAP=\(\angle\)OBP (প্রত্যেকে 1 সমকোণ)
অতিভূজ OP সাধারণ বাহু
এবং OA=OB (একই বৃত্তের ব্যাসার্ধ)
∴ ∆PAO≅∆PBO [সর্বসমতার R-H-S শর্তানুসারে]
∴ PA=PB(সর্বসম ত্রিভূজের অনুরূপ বাহু) ----[(i) প্রমাণিত]
এবং \(\angle\)POA=\(\angle\)POB (সর্বসম ত্রিভূজের অনুরূপ কোণ) ----[(ii) প্রমাণিত]