পাশের চিত্রে, LM || AB এবং AL= (x-3) একক, AC = 2x একক, BM = (x-2) একক এবং BC= (2x + 3) একক হলে, x-এর মান নির্ণয় করি।
Loading content...
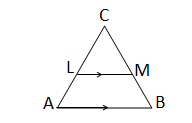
\(∵LM∥AB\)
\(∴\cfrac{CL}{AL}=\cfrac{CM}{BM} \)
বা,\(\cfrac{AC-AL}{AL}=\cfrac{BC-BM}{BM} \)
বা,\(\cfrac{2x-(x-3)}{(x-3)}=\cfrac{(2x+3)-(x-2)}{(x-2)} \)
বা,\(\cfrac{2x-x+3}{(x-3)}=\cfrac{2x+3-x+2}{(x-2)} \)
বা,\(\cfrac{(x+3)}{(x-3)}=\cfrac{(x+5)}{(x-2)} \)
বা,\((x+3)(x-2)=(x-3)(x+5)\)
বা,\(x^2-2x+3x-6=x^2+5x-3x-15\)
বা,\(x^2+x-x^2-2x=-15+6 \)
বা,\(-x=-9\)
বা, \(x=9 \)
∴নির্নেয় মান, \(x=9\)(Answer)