দুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে।A বিন্দুগামী সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ΔBCD সমবাহু ত্রিভুজ।
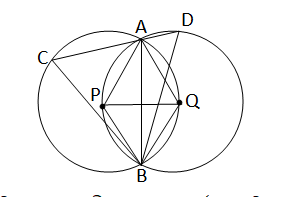
ধরি,P ও Q কেন্দ্রীয় সমান ব্যাসার্ধের বৃত্তদুটি একে অপরের কেন্দ্রগামী এবং পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা বৃত্তদুটিকে C এবং D বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,∆BCD একটি সমবাহু ত্রিভূজ।
অঙ্কনঃ A,B;P,Q;A,P;B,P;A,Q;B,Q যোগ করা হল।
প্রমানঃ ∆APQ এর AP=PQ=AQ [বৃত্তের ব্যাসার্ধ]
∴∆APQ একটি সমবাহু ত্রিভূজ
∴∠APQ=∠AQP=∠PAQ=60°
আবার,∆BPQ এর BP=PQ=BQ [বৃত্তের ব্যাসার্ধ]
∴∠BPQ=∠BQP=∠PBQ=60°
∴∠APQ+∠BPQ=∠AQP+∠BQP=60°+60°
অর্থাৎ,∠APB=∠AQB=120°
এখন,P কেন্দ্রীয় বৃত্তের AQB চাপের ওপর অবস্থিত
কেন্দ্রীয় কোণ ∠APB এবং বৃত্তস্থ কোণ ∠ACB
∴∠ACB=\(\frac{∠APB}{2}=\frac{120°}{2}\)=60°
আবার,Q কেন্দ্রীয় বৃত্তের APB চাপের ওপর অবস্থিত
কেন্দ্রীয় কোণ ∠AQB এবং বৃত্তস্থ কোণ ∠ADB
∴∠ADB=\(\frac{∠AQB}{2}=\frac{120°}{2}\)=60°
∆BCD এর,∠CBD=180°-(∠DCB+∠CDB)
=180°-(60°+60°)=60°
∴ ∆BCD এর ∠DCB=∠CDB= ∠CBD
∴∆BCD একটি সমবাহু ত্রিভূজ (প্রমানিত)