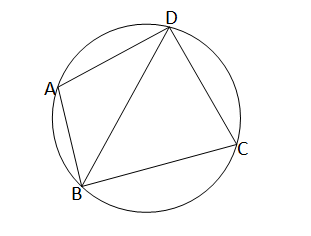
ABCD একটি বৃত্তস্থ চতুর্ভুজ। \(\angle\)ADB = \(x°\) এবং \(\angle\)ABD = \(y°\) হলে \(\angle\)BCD এর মান হবে \( (x + y)° \) Madhyamik 2025
Loading content...
বিবৃতিটি সত্য ।
\(\triangle\)ABD এর \(\angle\)ADB = \(x°\) এবং \(\angle\)ABD = \(y°\)
\(\therefore \angle\)BAD=180\(^o\)-(\(\angle\)ADB+\(\angle\)ABD)
অর্থাৎ, \(\angle\)BAD=180\(^o\)-(\(x°+y°\)) \(-----(i)\)
আবার যেহেতু, ABCD একটি বৃত্তস্থ ত্রিভূজ
\(\therefore \angle\)BAD+\(\angle\)BCD=180\(^o\)
বা, \(\angle\)BCD=180\(^o\)-\(\angle\)BAD \(-----(ii)\)
বা, \(\angle\)BCD=180\(^o\)-[180\(^o\)-(\(x°+y°\))]
\(\therefore \angle\)BCD=(\(x+y\))\(^o\)