যদি ABCD বৃত্তস্থ চতুর্ভুজের AB = DC হয়, তবে প্রমাণ করি যে AC = BD হবে।
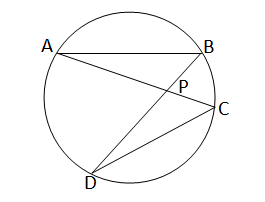
বৃত্তের AB এবং DC দুটি সমান দৈর্ঘ্যের জ্যা। প্রমান করতে হবে যে,AC=BD
অঙ্কনঃ A,C এবং B,D যুক্ত করা হল। AC এবং BD পরস্পরকে P বিন্দুতে ছেদ করল ।
প্রমানঃ যেহেতু,∠BAC এবং ∠BDC একই বৃত্তাংশের ওপর অবস্থিত,তাই ∠BAC=∠BDC
অর্থাৎ,∠BAP=∠PDC
এখন ∆APB এবং ∆DPC এর মধ্যে
AB=DC [প্রদত্ত]
∠APB=বিপ্রতীপ ∠DPC
এবং ∠BAP=∠PDC [পূর্বে প্রমানিত]
∴∆APB ≅ ∆DPC
∴AP=DP এবং PB=PC [অনুরূপ বাহু]
∴AP+PC=DP+PB
অর্থাৎ, AC=BD (প্রমানিত)