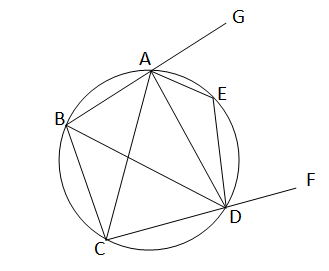
---

বৃত্তস্থ ABCD চতুর্ভূজের \(\angle\)BDC এর বর্হিদ্বিখন্ডক DE জ্যা। প্রমান করতে হবে যে,AE,\(\angle\)BAC এর বর্হিদ্বিখন্ডক

অঙ্কনঃ CD কে F পর্যন্ত এবং BA কে G পর্যন্ত বর্ধিত করা হল।

প্রমানঃ বৃত্তস্থ চতুর্ভূজ AEDB থেকে পাই
∵বৃত্তস্থ চতুর্ভূজের বহিঃস্থ কোণ বিপরীত কোণের সমান
∴\(\angle\)EAG=\(\angle\)EDB

আবার যেহেতু ED,\(\angle\)BDC এর বর্হিদ্বিখন্ডক তাই,
\(\angle\)EDB=\(\angle\)EDF
∴\(\angle\)EAG=\(\angle\)EDF---(i)

আবার,বৃত্তস্থ চতুর্ভূজ ACDE থেকে পাই
∵বৃত্তস্থ চতুর্ভূজের বহিঃস্থ কোণ বিপরীত কোণের সমান
∴\(\angle\)EDF=\(\angle\)EAC---(ii)

(i)এবং (ii)নং সমীকরন থেকে পাই
\(\angle\)EAG=\(\angle\)EAC
∴AE,\(\angle\)BAC এর বর্হিদ্বিখন্ডক (প্রমানিত)