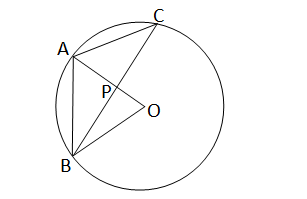
---

O কেন্দ্রীয় বৃত্তে,AB=AC=6 সেমি,
∵সমান দৈর্ঘ্যবিশিষ্ট জ্যা এর মধ্যবর্তী কোণের সমদ্বিখন্ডক কেন্দ্রগামী হয়,
তাই,OA=বৃত্তের ব্যাসার্ধ=5 সেমি
এবং P,BC এর মধ্যবিন্দু ও OP⊥BC ;
O,B যোগ করা হল।

ধরি,OP=\(x\) সেমি,
সমকোণী ∆APB থেকে পাই,
AP\(^2\)+BP\(^2\)=AB\(^2\)
বা, BP\(^2\)=AB\(^2\)-AP\(^2\)=6\(^2\)-AP\(^2--(i)\)

সমকোণী ∆OPB থেকে পাই,
OP\(^2\)+BP\(^2\)=OB\(^2\)
বা, BP\(^2\)=OB\(^2\)-OP\(^2\)=5\(^2\)-OP\(^2--(ii)\)

\((i)\) এবং \((ii)\) নং সমীকরন থেকে পাই
6\(^2\)-AP\(^2\)= 5\(^2\)-OP\(^2\)
বা,36-(OA-OP)\(^2\)=5\(^2\)-OP\(^2\)
বা,36-(5-x)\(^2\)=25-x\(^2\)
বা,36-(25-10x+x\(^2\) )=25-x\(^2\)
বা,36-25+10x-x\(^2\)=25-x\(^2\)
বা,11+10x=25
বা,10x=25-11
বা,x=\(\frac{14}{10}=\frac{7}{5}\)
∴OP=\(\frac{7}{5}\) সেমি

\((ii)\) নং সমীকরনে OP এর মান বসিয়ে পাই,
BP\(^2\)=5\(^2\)-\((\frac{7}{5})^2\)=25-\(\frac{49}{25}=\frac{625-49}{25}=\frac{536}{25}\)
বা, BP=\(\sqrt{\frac{536}{25}}=\frac{24}{5}\)

∴BC=2BP=2×\(\frac{24}{5}=\frac{48}{5}\)=9.6 সেমি (Answer)