5√3 মিটার উঁচু একটি রেলওয়ে ওভারব্রিজে দাঁড়িয়ে এক ব্যক্তি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন । কিন্তু 2 সেকেন্ড পরে ওই ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন । ট্রেনটির গতিবেগ কত ? Madhyamik 2018
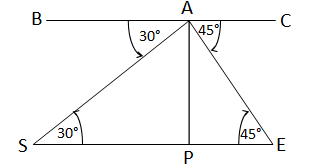
ধরি, ওই ব্যক্তি BC রেলওয়ে ওভারব্রিজের A বিন্দুতে দাঁড়িয়ে ট্রেনের ইঞ্জিনটিকে প্রথমে S বিন্দুতে এবং 2 সেকেন্ড পরে E বিন্দুতে দেখলেন। অবনতি কোণ ∠BAS=30° এবং ∠CAE=45°,
AP=রেলওয়ে ওভারব্রিজের উচ্চতা=5√3 মিটার
আবার যেহেতু BC||SE
তাই,∠ASP=একান্তর ∠BAS=30°
এবং ∠AEP=একান্তর ∠CAE=45°
সমকোণী ত্রিভূজ ASP থেকে পাই
tan30°=\(\cfrac{AP}{SP}=\cfrac{5√3}{SP}\)
বা, \(\cfrac{1}{√3}=\cfrac{5√3}{SP}\)
বা, \(SP=15 \)
সমকোণী ত্রিভূজ APE থেকে পাই,
tan45°= \(\cfrac{AP}{PE}=\cfrac{5√3}{PE}\)
বা, \(1=\cfrac{5√3}{PE}\)
বা, \(PE=5√3\)
∴2 সেকেন্ডে ট্রেনটির অতিক্রান্ত পথ=SE
=SP+PE=15+5√3
=15+(5×1.732)=15+8.660
=23.660 মিটার
∴ট্রেনটির গতিবেগ=\(\cfrac{23.660}{2}\) মিটার/সেকেন্ড=\(11.83\) মিটার/সেকেন্ড (প্রায়)