কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে। P, S ও R, Q যুক্ত করে, প্রমাণ করি যে, ∆PXS ও ∆RSQ সদৃশকোণী। এর থেকে প্রমাণ করি যে, PX.XQ=RX.XS <br/> অথবা একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।

কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে। P, S ও R, Q যুক্ত করে, প্রমাণ করি যে, ∆PXS ও ∆RSQ সদৃশকোণী। এর থেকে প্রমাণ করি যে, PX.XQ=RX.XS
অথবা একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।

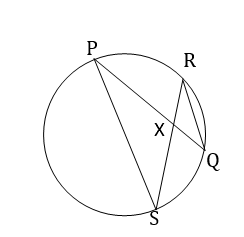
ধরি বৃত্তের PQ এবং RS জ্যা দুটি পরস্পরকে X বিন্দুতে ছেদ করেছে। প্রমান করতে হবে যে,∆PXS ও ∆RXQ সদৃশকোণী এবং PX.XQ=RX.XS

প্রমানঃ ∆PXS এবং ∆RXQ এর মধ্যে
∠SPQ=∠SRQ [একই বৃত্তচাপে অবস্থিত]
অর্থাৎ,∠SPX=∠XRQ
∠PSR=∠PQR [একই বৃত্তচাপে অবস্থিত]
অর্থাৎ,∠PSX=∠RQX
এবং ∠PXS=বিপ্রতীপ∠RXQ
∴∆PXS এবং ∆RXQ সদৃশকোণী।

∴\(\frac{PX}{RX}=\frac{XS}{XQ}=\frac{PS}{RQ}\)
অর্থাৎ, \(\frac{PX}{RX}=\frac{XS}{XQ}\)
বা,PX.XQ=RX.XS (প্রমানিত)