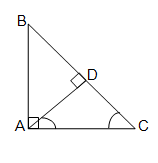
---

চিত্র থেকে পাই, ত্রিভূজ ACD এর ∠ADC সমকোণ [যেহেতু সমদ্বিবাহু ত্রিভূজের সমান বাহুদ্বয়ের অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক বিপরীত বাহুকে সমকোণে সমদ্বিখন্ডিত করে ।]

∴ সমকোণী ত্রিভূজ ADC থেকে ∠ACD এর সাপেক্ষে পাই
sec∠ACD= অতিভূজ/ভূমি \(=\frac{AC}{DC}\)

এবং ∠CAD এর সাপেক্ষে পাই,
sin∠CAD= লম্ব/অতিভূজ \(=\frac{DC}{AC}\)
∴বামপক্ষ= \(\cfrac{sec∠ACD}{sin∠CAD}=\cfrac{\frac{AC}{DC}}{\frac{DC}{AC}}=\left(\cfrac{AC}{DC}\right)^2\)

এবং,ডানপক্ষ \(=cosec^2∠CAD\)
=(অতিভূজ/লম্ব)\(^2\)
\(=\left(\cfrac{AC}{DC}\right)^2\)

∴ বামপক্ষ=ডানপক্ষ (প্রমাণিত)