O কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু। এবার A, C; B, C এবং O, C যুক্ত করে দেখাই যে, tan ∠ABC=cot ∠ACO
Loading content...
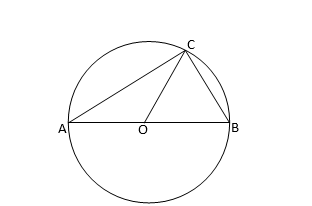
আমরা জানি,অর্ধবৃত্তস্থ কোন সমকোন ।
∴∠ACB=90°
সতরাং ∠ABC ও ∠CAB পরস্পর পূরক কোন।
আবার ∆AOC এর
OA=OC [উভয়েই বৃত্তের ব্যাসার্ধ ]
∴∠ACO=∠CAO
এখন tan∠ABC
=tan(90°-∠CAB)
=tan(90°-∠CAO)
=tan(90°-∠ACO) [∵ ∠ACO=∠CAO]
=cot∠ACO (প্রমানিত)