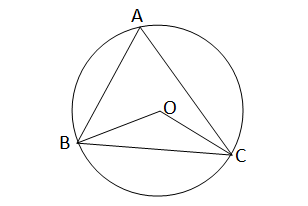
---

∆ABC এর পরিকেন্দ্র O;
প্রমান করতে হবে যে,\(\angle\)OBC+\(\angle\)BAC=90°

অঙ্কনঃ O,C যুক্ত করা হল।

প্রমানঃ ∆OBC থেকে পাই,
\(\angle\)OBC=\(\angle\)OCB [∵OB=OC=বৃত্তের ব্যাসার্ধ]
\(\angle\)BOC+\(\angle\)OBC+\(\angle\)OCB=180°
বা,2\(\angle\)OBC+\(\angle\)BOC=180°---(i)

আবার BC চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)BOC
এবং বৃত্তস্থ কোণ \(\angle\)BAC
∴\(\angle\)BOC=2\(\angle\)BAC
(i)নং সমীকরনে \(\angle\)BOC এর মান বসিয়ে পাই
2\(\angle\)OBC+2\(\angle\)BAC=180°
বা,\(\angle\)OBC+\(\angle\)BAC=90° (প্রমানিত)