ABCD একটি বৃত্তস্থ চতুর্ভুজ। DE জ্যা ∠BDC-এর বহির্দ্বিখণ্ডক। প্রমাণ করি যে, AE (বা বর্ধিত AE) ∠BAC-এর বহির্দ্বিখণ্ডক।
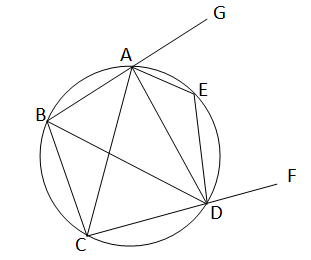
বৃত্তস্থ ABCD চতুর্ভূজের \(\angle\)BDC এর বর্হিদ্বিখন্ডক DE জ্যা। প্রমান করতে হবে যে,AE,\(\angle\)BAC এর বর্হিদ্বিখন্ডক
অঙ্কনঃ CD কে F পর্যন্ত এবং BA কে G পর্যন্ত বর্ধিত করা হল।
প্রমানঃ বৃত্তস্থ চতুর্ভূজ AEDB থেকে পাই
∵বৃত্তস্থ চতুর্ভূজের বহিঃস্থ কোণ বিপরীত কোণের সমান
∴\(\angle\)EAG=\(\angle\)EDB
আবার যেহেতু ED,\(\angle\)BDC এর বর্হিদ্বিখন্ডক তাই,
\(\angle\)EDB=\(\angle\)EDF
∴\(\angle\)EAG=\(\angle\)EDF---(i)
আবার,বৃত্তস্থ চতুর্ভূজ ACDE থেকে পাই
∵বৃত্তস্থ চতুর্ভূজের বহিঃস্থ কোণ বিপরীত কোণের সমান
∴\(\angle\)EDF=\(\angle\)EAC---(ii)
(i)এবং (ii)নং সমীকরন থেকে পাই
\(\angle\)EAG=\(\angle\)EAC
∴AE,\(\angle\)BAC এর বর্হিদ্বিখন্ডক (প্রমানিত)