কোনো বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের উপর অঙ্কিত লম্ব PAQ-কে Z বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, XA, ∠XYZ-এর সমদ্বিখণ্ডক।
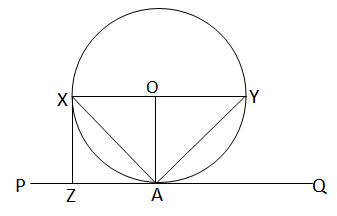
বৃত্তটির XY ব্যাস। বৃত্তটির ওপর A বিন্দুতে PQ ব্যাস। X বিন্দু থেকে PQ এর ওপর লম্ব Z বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,XA,\(\angle\)YXZ এর সমদ্বিখন্ডক।
অঙ্কনঃ O,A যুক্ত করা হল।
প্রমানঃ ∆OAX এর
OX=OA[উভয়েই বৃত্তের ব্যাসার্ধ]
∴\(\angle\)OXA=\(\angle\)OAX
আবার,যেহেতু PQ,A বিন্দুতে স্পর্শক।
∴\(\angle\)OAZ=90°
অর্থাৎ,\(\angle\)OAX+\(\angle\)XAZ=90°---(i)
∵XZ⊥PQ
∴\(\angle\)ZXA+\(\angle\)XAZ=90°---(ii)
(i)এবং (ii) নং সমীকরন থেকে পাই,
\(\angle\)OAX+\(\angle\)XAZ=\(\angle\)ZXA+\(\angle\)XAZ
অর্থাৎ,\(\angle\)OAX=\(\angle\)ZXA
বা,\(\angle\)OXA=\(\angle\)ZXA [∵\(\angle\)OXA=\(\angle\)OAX]
∴XA,\(\angle\)YXZ এর সমদ্বিখন্ডক। (প্রমানিত)