একটি বৃত্তের দুটি পরস্পরছেদী জ্যা-এর অন্তর্ভূক্ত কোণের সমদ্বিখন্ডক যদি কেন্দ্রগামী হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি সমান।
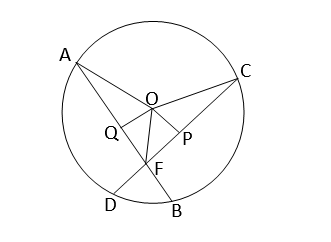
O কেন্দ্রীয় বৃত্তে AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা পরস্পরকে F বিন্দুতে ছেদ করেছে। OF,∠AFC এর সমদ্বিখন্ডক হলে প্রমান করতে হবে যে,AB=CD
অঙ্কনঃ O বিন্দু থেকে AB ও CD এর উপর লম্ব OQ এবং OP আঁকা হল। O,A এবং O,C যুক্ত করা হল।
প্রমানঃ ∆OQF এবং ∆OFP এর মধ্যে,
∠OQF=∠OPF [উভয়েই লম্ব]
∠OFQ=∠OFP [∵OF,∠AFC এর সমদ্বিখন্ডক]
OF সাধারন
∴∆OQF ≅ ∆OFP
∴OQ=OP (অনুরূপ বাহু)
আবার ∆OAQ এবং ∆OCP এর মধ্যে,
∠OQA=∠OPC [উভয়েই লম্ব]
OA=OC(বৃত্তের ব্যাসার্ধ)
এবং OQ=OP (পূর্বে প্রমানিত)
∴ ∆OAQ ≅ ∆OCP
∴AQ=CP(অনুরূপ বাহু)
∵ বৃত্তের কেন্দ্র থেকে ব্যাস নয় এরূপ কোনো জ্যা এর ওপর লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে
∴AQ=\(\cfrac{1}{2}\) AB এবং CP=\(\cfrac{1}{2}\) CD
∴ \(\cfrac{1}{2}\) AB=\(\cfrac{1}{2}\) CD
বা, AB=CD (প্রমানিত)