সূর্যের উন্নতি কোণ 45° হলে, কোনো সমতলে অবস্থিত একটি স্তম্ভের ছায়ার দৈর্ঘ্য যা হয়, উন্নতি কোণ 30° হলে, ছায়ার দৈর্ঘ্য তার চেয়ে 60 মিটার বেশি হয়। স্তম্ভটির উচ্চতা নির্ণয় করি। Madhyamik 2015
Loading content...
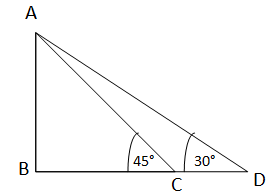
ধরি,সূর্যের উন্নতি কোণ যখন 45° থাকে,তখন তার ছায়ার দৈর্ঘ্য হয় BC এবং সূর্যের উন্নতি কোণ যখন 30° হয়,তখন তার ছায়ার দৈর্ঘ্য হয় BD এবং বর্দ্ধিত ছায়ার দৈর্ঘ্য CD=60 মিটার ।
সমকোণী ত্রিভূজ ABC থেকে পাই,
\(tan45°=\) লম্ব / ভূমি \(=\cfrac{AB}{BC}\)
বা, \(1= \cfrac{AB}{BC}\)
বা, \(AB=BC\)----(i)
সমকোণী ত্রিভূজ ABD থেকে পাই
\(tan30° =\) লম্ব / ভূমি \(=\cfrac{AB}{BD}\)
বা,\(\cfrac{1}{\sqrt3}=\cfrac{AB}{BD}\)
বা, \(AB=\cfrac{BD}{\sqrt3}\)----(ii)
(i)এবং (ii) নং সমীকরনে AB এর মান তুলনা করে পাই
\(BC=\cfrac{BD}{\sqrt3}\)
বা,\(\sqrt3 BC=BD\)
বা, \(\sqrt3 BC=(BC+CD)\)
বা, \(\sqrt3 BC-BC=CD\)
বা, \(BC(\sqrt3-1)=60\)
বা, \(BC=\cfrac{60}{(\sqrt3-1)}\)
বা, \(BC=\cfrac{60(\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}\)
বা, \(BC=\cfrac{60(\sqrt3+1)}{3-1}\)
বা, \(BC=\cfrac{\cancel{60}30(\sqrt3+1)}{\cancel2}\)
বা, \(BC=30(\sqrt3+1)\)
(i) নং সমীকরনে BC এর মান বসিয়ে পাই
AB=BC=\(30(\sqrt3+1)\)
∴স্তম্ভটির উচ্চতা \(30(\sqrt3+1)\) মিটার ।
