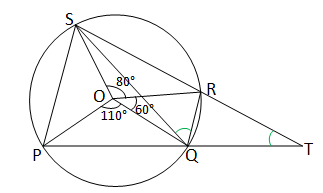
---

∵SR বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)ROS এবং পরিধিস্থ কোণ \(\angle\)RQS
∴2\(\angle\)RQS=\(\angle\)ROS=80°
অর্থাৎ,\(\angle\)RQS=40°

আবার,\(\angle\)POS=360°-(110°+60°+80°)=360°-250°=110°

SP চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)SOP এবং পরিধিস্থ কোণ \(\angle\)SQP
∴\(\angle\)SQP=\(\frac{1}{2}\)\(\angle\)SOP=\(\frac{110°}{2}\)=55°
∴\(\angle\)POR=\(\angle\)RQS+\(\angle\)SQP=40°+55°=95°
∴\(\angle\)PSR=180°-\(\angle\)POR=180°-95°=85° [∵বৃত্তস্থ চতুর্ভূজের বিপরীত কোণ]

আবার SRQ চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)SOQ এবং পরিধিস্থ কোণ \(\angle\)SPQ
∴\(\angle\)SPQ=\(\frac{1}{2}\)\(\angle\)SOQ=\(\frac{1}{2}\) (\(\angle\)QOR+\(\angle\)ROS)
=\(\frac{1}{2}\) (60°+80°)=\(\frac{140°}{2}\)=70°

∆SPT থেকে পাই,
\(\angle\)PTS=180°-(\(\angle\)PST+\(\angle\)SPT)
=180°-(85°+70°)=180°-155°=25°

∴\(\angle\)QTR=\(\angle\)PTS=25° [একই কোণ]