কোনো বৃত্তের AC ও BD দুটি জ্যা পরস্পরকে O বিন্দুতে ছেদ করেছে। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ∠P + ∠Q = 2∠BOC.
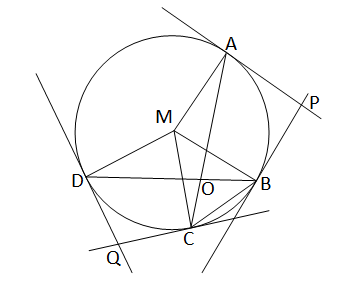
ধরি,বৃত্তের AC ও BD দুটি জ্যা পরস্পরকে O বিন্দুতে ছেদ করেছে । A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,\(\angle\)P+\(\angle\)Q=2\(\angle\)BOC
অঙ্কনঃ ধরি M বৃত্তের কেন্দ্র। M,A;M,B;M,C এবং M,D ও B,C যুক্ত করা হল।
প্রমানঃ চতুর্ভূজ AMBP এর
\(\angle\)MAP=\(\angle\)MBP=90°
∴\(\angle\)MAP+\(\angle\)MBP=180°
∴AMBP সমবৃত্তস্থ
অর্থাৎ,\(\angle\)P+\(\angle\)AMB=180°
বা,\(\angle\)P+2\(\angle\)ACB=180° [∵AB চাপের ওপর \(\angle\)AMB কেন্দ্রস্থ এবং \(\angle\)ACB পরিধিস্থ কোণ)]
বা,2\(\angle\)ACB=180°-\(\angle\)P---(i)
একইভাবে প্রমান করা যায় যে,
2\(\angle\)DBC=180°-\(\angle\)Q---(ii)
আবার ∆OCB এর
\(\angle\)OCB+\(\angle\)OBC+\(\angle\)BOC=180°
বা,2\(\angle\)OCB+2\(\angle\)OBC+2\(\angle\)BOC=360° [উভয়পক্ষকে 2 দ্বারা গুন করে পাই]
বা,[180°-\(\angle\)P]+[180°-\(\angle\)Q]+2\(\angle\)BOC=360°[(i)এবং (ii)নং সমীকরনের মান বসিয়ে]
বা,2\(\angle\)BOC=\(\angle\)P+\(\angle\)Q (প্রমানিত)