প্রমাণ করি যে একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির যে-কোনোটিকে ব্যাস করে অঙ্কিত বৃত্ত অসমান বাহুটিকে সমদ্বিখণ্ডিত করে।
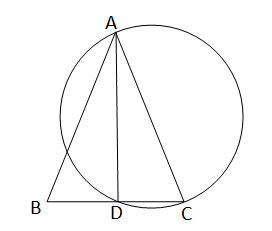
ধরি,∆ABC এর AB=AC এবং AC বাহুকে ব্যাস ধরে অঙ্কিত বৃত্ত অসমান বাহু BC কে D বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,D,BC এর মধ্যবিন্দু।
অঙ্কনঃ A,D যুক্ত করা হল।
প্রমানঃ∵AC বৃত্তের ব্যাস।
সুতরাং,\(\angle\)ADC=90°
এখন ∆ABD এবং ∆ADC এর মধ্যে,
AB=AC (প্রদত্ত)
\(\angle\)ADB=\(\angle\)ADC (উভয়েই সমকোণ)
AD সাধারন।
∴∆ABD \(\cong\) ∆ADC
∴BD=DC (অনুরূপ বাহু)
∴D,BC এর মধ্যবিন্দু (প্রমানিত)