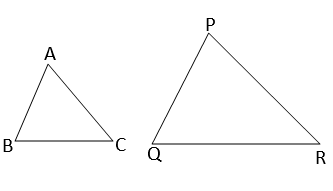
---

মনে করি , \(\triangle\)ABC এবং \(\triangle\)PQR দুটি সদৃশ ত্রিভূজ

প্রমান করতে হবে যে , \(\triangle\)ABC এর পরিসীমা / \(\triangle\)PQR এর পরিসীমা =\(\cfrac{AB}{PQ}=\cfrac{BC}{QR}=\cfrac{CA}{RP}\)

প্রমান:- \(\triangle\)ABC ও \(\triangle\)PQR সদৃশ ।
\(\therefore \cfrac{AB}{PQ}=\cfrac{BC}{QR}=\cfrac{CA}{RP}\)
সুতরাং \(\cfrac{AB}{PQ}=\cfrac{BC}{QR}=\cfrac{CA}{RP} =\cfrac{AB+BC+CA}{PQ+QR+RP}\) [সংযোজন প্রক্রিয়া করে পাই]

\(\therefore \triangle\)ABC এর পরিসীমা / \(\triangle\)PQR এর পরিসীমা =\(\cfrac{AB}{PQ}=\cfrac{BC}{QR}=\cfrac{CA}{RP}\) [প্রমানিত]