A ও B কেন্দ্রীয় দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে C বিন্দুতে বহিঃস্পর্শ করেছে। C বিন্দুতে অঙ্কিত স্পর্শকের উপর O একটি বিন্দু এবং OD ও OE যথাক্রমে A ও B কেন্দ্রীয় বৃত্তকে যথাক্রমে D ও E বিন্দুতে স্পর্শ করেছে । ∠COD = 56°, ∠COE = 40°, ∠ACD = x° এবং ∠BCE = y° হলে প্রমাণ করি যে OD = OC = OE এবং x-y = ৪
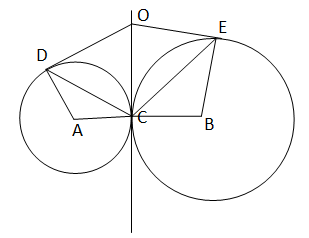
ACOD চতুর্ভূজের \(\angle\)ADO এবং \(\angle\)ACO প্রত্যেকে 90°
যেহেতু,OD এবং OC,A কেন্দ্রীয় বৃত্তের স্পর্শক।
∴\(\angle\)DAC+\(\angle\)DOC=180°
বা,\(\angle\)DAC=(180°-56°)=124°
আবার যেহেতু,DA=AC(বৃত্তের ব্যাসার্ধ)
∴\(\angle\)ADC=\(\angle\)DCA=(180°-124°)/2=28°
\(\angle\)ODC=90°-28°=62° এবং
\(\angle\)OCD=90°-28°=62°
∴\(\angle\)ODC=\(\angle\)OCD
∴∆ODC একটি সমদ্বিবাহু ত্রিভূজ,অর্থাৎ,OD=OC
BCOE চতুর্ভূজের \(\angle\)BCO এবং \(\angle\)BEO প্রত্যেকে 90°
যেহেতু,OE এবং OC,B কেন্দ্রীয় বৃত্তের স্পর্শক।
∴\(\angle\)CBE+\(\angle\)COE=180°
বা,\(\angle\)CBE=(180°-40°)=140°
আবার যেহেতু,BC=BE(বৃত্তের ব্যাসার্ধ)
∴\(\angle\)BCE=\(\angle\)BEC=(180°-140°)/2=20°
\(\angle\)OCE=90°-20°=70° এবং
\(\angle\)OEC=90°-20°=70°
∴\(\angle\)OCE=\(\angle\)OEC
∴∆OCE একটি সমদ্বিবাহু ত্রিভূজ,অর্থাৎ,OC=OE
∴OD=OC=OE (প্রমানিত)
আবার,x°-y°=\(\angle\)ACD-\(\angle\)BCE
=70°-62°=8°
∴x-y=8 (প্রমানিত)