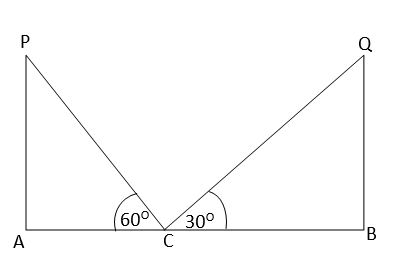
---

ধরি, AB=120 মিটার চওড়া রাস্তার দুপাশে ঠিক বিপরীতে A ও B বিন্দুতে দুটি সমান উচ্চতার স্তম্ভ আছে । স্তম্ভদুটির পাদবিন্দুর সংযোগ রেখা AB-এর উপর C বিন্দু থেকে A ও B বিন্দুতে স্তম্ভ দুটির শীর্ষ যথাক্রমে P এবং Q বিন্দুদ্বয়ের উন্নতি কোণ যথাক্রমে \(\angle ACP=60^o\) ও \(\angle BCQ=30^o\) ।

এখন AC এর মান নির্ণয় করতে হবে ।

\(\triangle APC\) থেকে পাই,
\(\cfrac{AP}{AC}=tan 60^o\)
বা, \( \cfrac{AP}{AC}=\sqrt3\)
বা, \( AC=\cfrac{AP}{\sqrt3} -----(i)\)

আবার, \(\triangle BCQ\) থেকে পাই,
\(\cfrac{BQ}{BC}=tan 30^o\)
বা, \( \cfrac{BQ}{BC}=\cfrac{1}{\sqrt3}\)
বা, \( BC=\sqrt3 BQ\)
বা, \( BC=\sqrt3 AP -----(ii) [\because AP=BQ]\)

আমরা জানি, \(AB=120\)
বা, \(AC+BC=120\)
বা, \(\cfrac{AP}{\sqrt3}+\sqrt3 AP=120 [(i)\) এবং \((ii)\) নং সমীকরনের মান বসিয়ে \(]\)
বা, \(AP\left(\sqrt3+\cfrac{1}{\sqrt3}\right)=120\)
বা, \(AP\left(\cfrac{3+1}{\sqrt3}\right)=120\)
বা, \(AP=\cfrac{120\times \sqrt3}{4}=30\sqrt3\)

\((i)\) নং সমীকরনে \(AP\) এর মান বসিয়ে পাই, \( AC=\cfrac{30\sqrt3}{\sqrt3}=30 \)

\(\therefore AC\) এর মান \(30\) মিটার ।