প্রমাণ করি, একটি বৃত্তে দুটি জ্যা-এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবর্তী সেটির দৈর্ঘ্য অপর জ্যা-টির দৈর্ঘ্য অপেক্ষা বৃহত্তর।
Loading content...
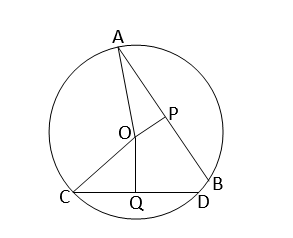
ধরি,O কেন্দ্রীয় বৃত্তের AB এবং CD দুটি জ্যা,যাদের কেন্দ্র থেকে দূরত্ব যথাক্রমে OP ও OQ এবং OP
অঙ্কনঃ O,A এবং O,C যুক্ত করা হল।
প্রমানঃ∵OP⊥AB
∴AP=\(\frac{1}{2}\) AB
∴সমকোণী ∆AOP এর OA\(^2\)=OP\(^2\)+AP\(^2\)
আবার,OQ⊥AB
∴CQ=\(\frac{1}{2}\) CD
এবং সমকোণী ∆COQ এর OC\(^2\)=OQ\(^2\)+CQ\(^2\)
∵OA=OC=বৃত্তের ব্যাসার্ধ
∴OP\(^2\)+AP\(^2\)=OQ\(^2\)+CQ\(^2\)
∵OP
বা,AP>CQ
বা,\(\frac{1}{2}\) AB>\(\frac{1}{2}\) CD
বা,AB>CD (প্রমানিত)
