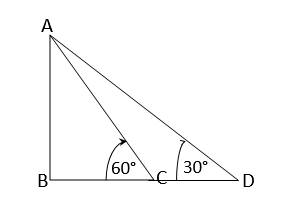
---

ধরি,AB চিমনির গোড়ার সমতলে একটি বিন্দু C থেকে চিমনির চূড়া A বিন্দুর উন্নতি কোণ ∠ACB=60° এবং C বিন্দু থেকে 24 মিটার দূরের একটি বিন্দু D এর সাপেক্ষে চিমনির চূড়া A এর উন্নতি কোণ ∠ADB =30° এবং CD=24 মিটার ।

ত্রিভূজ ABC থেকে ∠ACB এর পরিপ্রেক্ষিতে পাই
tan60°=লম্ব/ভূমি \(=\frac{AB}{BC}\)
বা,√3 \(=\frac{AB}{BC}\)
বা,AB=BC√3 \(---(i)\)

ত্রিভূজ ABD থেকে ∠ADB এর পরিপ্রেক্ষিতে পাই
tan30°=লম্ব/ভূমি \(=\frac{AB}{BD}\)
বা, \(\cfrac{1}{√3}=\frac{AB}{BD}\)
বা,AB \(=\frac{BD}{√3}---(ii)\)

\((i)\) এবং \((ii)\) সমীকরন থেকে পাই BC√3 \(=\frac{BD}{√3}\)
বা,BC√3 \(=\frac{BC+CD}{√3}\)
বা,3BC=BC+24
বা,3BC-BC=24
বা,2 BC=24
বা,BC=12

\((i)\) নং সমীকরনে BC=12 বসিয়ে পাই
AB=12√3=12×1.172=20.784

∴চিমনির উচ্চতা 20.784 মিটার ।