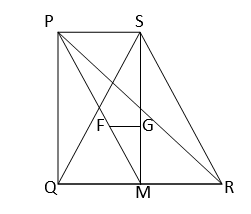
---

একই ভূমি \(QR\) একই পার্শ্বে অবস্থিত দুটি ত্রিভূজ \(∆PQR\) এবং \(∆SQR\) ,যাদের ক্ষেত্রফল সমান। \(F\) ও \(G\) ত্রিভূজ দুটির ভরকেন্দ্র হলে প্রমান করতে হবে যে, \(FG∥QR\)

অঙ্কনঃ \(P,S\) যুক্ত করা হল। \(P,F\) এবং \(S,G\) যুক্ত করে বর্ধিত করা হল যা \(QR\) কে \(M\) বিন্দুতে ছেদ করে।

প্রমানঃ \(∆PQR\) ত্রিভূজের \(PM\) মধ্যমা এবং \(∆SQR\) ত্রিভূজের \(SM\) মধ্যমা।
যেহেতু ত্রিভূজ দুটির ক্ষেত্রফল সমান এবং তারা \(QR \) এর একই পার্শ্বে অবস্থিত,তাই ত্রিভূজদুটি \(QR\) এবং \(PS\) সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত।

যেহেতু, \(F,∆PQR\) এর ভরকেন্দ্র এবং \(PM\) মধ্যমার ওপর অবস্থিত
\(∴ \cfrac{PF}{FM}= \cfrac{2}{1}\)

আবার যেহেতু, \(G, ∆SQR\) এর ভরকেন্দ্র এবং \(SM\) মধ্যমার ওপর অবস্থিত
\(∴ \cfrac{SG}{GM}= \cfrac{2}{1} \)

এখন \(∆PSM\) ত্রিভূজের
\( \cfrac{PF}{FM}= \cfrac{2}{1}= \cfrac{SG}{GM}\)
\(∴ PS∥FG\)

এখন \(PS∥QR\) এবং \(PS∥FG\)

\(∴ FG∥QR\) (প্রমানিত)